Neste tópico
- PPM < USL para desempenho "dentro" esperado
- PPM > USL para desempenho "dentro" esperado
- PPM total para desempenho "dentro" esperado
- Intervalos de confiança para PPM total relacionado ao desempenho "dentro" quando LSL e USL são valores conhecidos
- Intervalos de confiança para PPM total para o desempenho "dentro" para um processo com um limite de especificação
PPM < USL para desempenho "dentro" esperado

PPM < LSL e % < LSL são múltiplos da probabilidade:

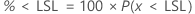
Intervalos de confiança bilaterais
Os intervalos de confiança para P(x < LSL) são dados pelas fórmulas a seguir:


em que
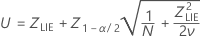
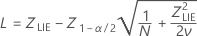

Os intervalos de confiança para PPM < LSL e% < LSL são encontrados multiplicando-se os intervalos de confiança da probabilidade por uma constante.
PPM


%
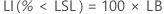
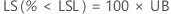
Limite de confiança unilateral
Para um limite unilateral, use os cálculos a seguir:

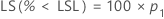
O Minitab resolve a seguinte equação para encontrar p1:
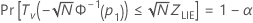
em que

Notação
Notação
| Termo | Descrição |
|---|---|
| LIE | o limite inferior de especificação |
| LSE | o limite superior de especificação |
| LI | o limite inferior |
| LS | o limite superior |
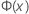 | a função de distribuição acumulada (FDA) de uma distribuição normal padrão |
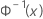 | a fda inversa de uma distribuição normal padrão |
 | o (1 - α/2)o percentil da distribuição normal padrão |
| α | o alfa para o nível de confiança |
 | a média do processo (estimada a partir dos dados da amostra ou de um valor histórico) |
| s | o desvio padrão da amostra dentro de subgrupos |
| N | o número total de medições |
| υ | os graus de liberdade para s |
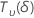 | uma variável aleatória que é distribuída como uma distribuição t não central com  graus de liberdade e parâmetro de não centralidade δ graus de liberdade e parâmetro de não centralidade δ |
PPM > USL para desempenho "dentro" esperado
As partes por milhão maiores que o limite superior de especificação (PPM > USL) e a porcentagem maior que o limite de especificação superior (% > USL) são encontradas a partir da probabilidade de uma parte estar acima do limite de especificação (P(x > USL)).

PPM > USL e % > USL são múltiplos da probabilidade:
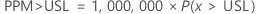
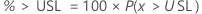
Intervalos de confiança bilaterais
Os intervalos de confiança para P(x > USL) são dados pelas fórmulas a seguir:


em que
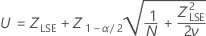
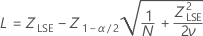

Os intervalos de confiança para PPM > USL e % > USL são encontrados multiplicando-se os intervalos de confiança da probabilidade por uma constante.
PPM


%
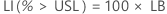
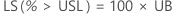
Limite de confiança unilateral
Para um limite unilateral, use os cálculos a seguir:

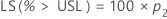
O Minitab resolve a seguinte equação para encontrar p1:
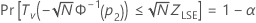
em que

Notação
| Termo | Descrição |
|---|---|
| LSE | o limite superior de especificação |
| PPM | as partes por milhão |
| LI | o limite inferior |
| LS | o limite superior |
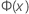 | a função de distribuição acumulada (FDA) de uma distribuição normal padrão |
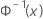 | a fda inversa de uma distribuição normal padrão |
 | o (1 - α/2)o percentil da distribuição normal padrão |
| α | o alfa para o nível de confiança |
 | a média do processo (estimada a partir dos dados da amostra ou de um valor histórico) |
| s | o desvio padrão da amostra dentro de subgrupos |
| N | o número total de medições |
| υ | os graus de liberdade para s |
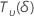 | uma variável aleatória que é distribuída como uma distribuição t não central com  graus de liberdade e parâmetro de não centralidade δ graus de liberdade e parâmetro de não centralidade δ |
PPM total para desempenho "dentro" esperado
O número esperado de partes por milhão que estão fora dos limites de especificação com base nos subgrupos dentro da variação é

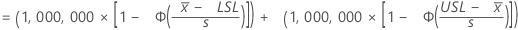
Notação
| Termo | Descrição |
|---|---|
| PPM | Partes por milhão |
| LSL | Limite inferior de especificação |
| USL | Limite superior de especificação |
| Φ (X) | A função distribuição acumulada (FDA) da distribuição normal padrão |
 | Média das observações |
| s | Desvio padrão dentro do subgrupo |
Intervalos de confiança para PPM total relacionado ao desempenho "dentro" quando LSL e USL são valores conhecidos
O total de Partes Por Milhão (PPM) que está fora de especificação e a porcentagem fora de especificação são ambos derivados da probabilidade de uma parte estar fora dos limites de especificação.
Intervalos de confiança bilaterais
Os limites superior e inferior para a probabilidade de uma parte estar fora de especificação têm as seguintes fórmulas:
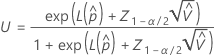
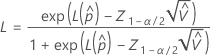
em que


Para calcular  , substitua as estimativas da amostra pelos parâmetros da fórmula para
, substitua as estimativas da amostra pelos parâmetros da fórmula para 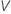 :
:



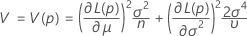
em que
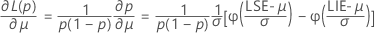

Os limites para o PPM total fora de especificação e para a porcentagem total fora de especificação são encontrados por meio da multiplicação dos limites para a probabilidade por uma constante.
PPM


%

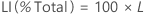
Limite de confiança unilateral
O limite superior para a probabilidade de uma parte estar fora de especificação tem a seguinte fórmula:
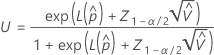
em que 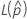 e
e  são os mesmos que para um intervalo de dois lados.
são os mesmos que para um intervalo de dois lados.
O limite superior para o PPM total fora de especificação e para a porcentagem fora de especificação são derivados da multiplicação do limite para a probabilidade por uma constante.
PPM

%

Notação
| Termo | Descrição |
|---|---|
| LIE | o limite inferior de especificação |
| LSE | o limite superior de especificação |
| PPM | as partes por milhão |
| LI | o limite inferior |
| LS | o limite superior |
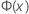 | a função de distribuição acumulada (FDA) de uma distribuição normal padrão |
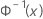 | a fda inversa de uma distribuição normal padrão |
 | a Função de Densidade de Probabilidade (FDP) de uma distribuição normal padrão |
 | o (1 - α / 2)o percentil da distribuição normal padrão |
| α | o alfa para o nível de confiança |
 | a média do processo (estimada a partir dos dados da amostra ou de um valor histórico) |
| s | o desvio padrão da amostra dentro de subgrupos |
| N | o número total de medições |
| υ | os graus de liberdade para s |
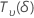 | Uma variável aleatória que é distribuída como uma distribuição t não central com  Graus de liberdade e parâmetro de não centralidade δ Graus de liberdade e parâmetro de não centralidade δ |
Intervalos de confiança para PPM total para o desempenho "dentro" para um processo com um limite de especificação
Para um processo com apenas um Limite Inferior de Especificação (LSL), o intervalo de confiança para o PPM total ou a porcentagem total fora de especificação é o mesmo que o intervalo de confiança para o PPM < LSL ou % < LSL. Acesse a seção em PPM < LSL para saber qual é o desempenho "dentro" esperado.
Para um processo com apenas um Limite Superior de Especificação (USL), o intervalo de confiança para o PPM total ou a porcentagem total fora de especificação é o mesmo que o intervalo de confiança para o PPM > USL ou % > USL. Acesse a seção em PPM > USL para saber qual é o desempenho "dentro" esperado.
