Medidas globais de capacidade
- Cnp
-
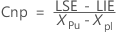
- Cnpl
-
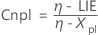
- Cnpu
-
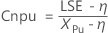
- Cnpk
- Cnpk = min{Cnpl, Cnpu}
Notação
| Termo | Descrição |
|---|---|
| LSE | Limite superior de especificação |
| LIE | Limite inferior de especificação |
| η | Mediana do processo |
| Xpu | Percentil empírico superior da tolerância |
| Xpl | Menor percentual empírico da tolerância |
Percentis empíricos
A análise utiliza os percentis empíricos para estimar a dispersão do processo. Primeiro, a análise usa a tolerância para encontrar os percentis a serem calculados.


onde Z é um percentil da distribuição normal padrão e T é a tolerância. Por exemplo, se a tolerância for 6, então pU = P(Z < 3) = 0.99865. Se a tolerância for 6, então pL = P(Z < −3) = 0.00135. Para um processo com 2 limites de especificação, uma tolerância de 6 cobre aproximadamente 99,7% dos dados.
Em seguida, a análise calcula os percentis empíricos a partir dos dados.

- Notação
-
Termo Descrição p a porcentagem de dados é menor ou igual ao percentil desejado, dividido por 100 Xy aésima linha y dos dados quando os dados são classificados do menor para o maior y o valor truncado de w w p(N + 1) N o número de linhas com dados não faltantes z w – y
Referências
McCormack, D. W., Harris, I. R., Hurwitz, A., M., & Spagon, P. D. (2000). Capability indices for non-normal data. Quality Engineering, 12(4), 489-495.
