Neste tópico
Etapa 1: Determine se o seu processo está estável
Antes de avaliar a capacidade de seu processo, determine se ele está estável. Se o processo não estiver estável, as estimativas de capacidade do processo podem não ser confiáveis.
Use a carta P para monitorar visualmente o %defeituosos e para determinar se %defeituosos está estável e sob controle.
Os pontos vermelhos indicam subgrupos que falharam em pelo menos um dos testes para causas especiais e não estão sob controle. Pontos fora de controle indicam que o processo pode não estar estável e que os resultados de uma análise de capacidade pode não ser confiável. Você deve identificar a causa de pontos fora de controle e eliminar as variações de causas especiais antes de analisar a capacidade do processo.

Nesta carta U, a maioria dos pontos varia de forma aleatória e está dentro dos limites de controle. Nenhuma tendência ou padrão está presente. A proporção de unidades defeituosas para o dia 19 está fora de controle. Antes de avaliar a capacidade do processo, investigue e elimine todas as causas especiais que possam ter contribuído para a taxa de defeituosos anormalmente elevada naquele dia.
Etapa 2: Determine se seus dados seguem uma distribuição binomial.
Antes de avaliar a capacidade de seu processo, determine se ele segue uma distribuição de binomial. Se os seus dados não seguem uma distribuição binomial, as estimativas de capacidade do processo podem não ser confiáveis. O gráfico que o Minitab mostra para avaliar a distribuição dos dados depende se os seus tamanhos dos subgrupos são iguais ou diferentes.
Os tamanhos dos subgrupos são iguais
Se os tamanhos de seus subgrupos forem todos iguais, o Minitab exibe um gráfico binomial.
Examine o gráfico para determinar se os pontos representados graficamente seguem aproximadamente uma linha reta. Se não, o pressuposto de que os dados foram amostrados a partir de uma distribuição binomial pode ser falso.
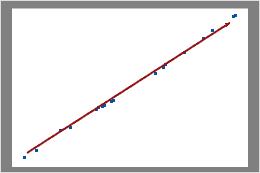
Binomial
Neste gráfico, os pontos de dados enquadram-se muito proximamente ao longo da linha. Você pode assumir que os dados seguem uma distribuição binomial.
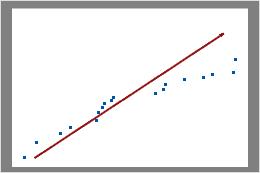
Não binomial
Neste gráfico, os pontos de dados não caem ao longo da linha perto da parte superior. Estes dados não seguem uma distribuição binomial e não podem ser avaliados de forma confiável usando análise de capacidade binomial.
Os tamanhos dos subgrupos não são iguais
Se os tamanhos de subgrupos variarem, o Minitab exibe um Gráfico de taxa de defeituosos.
Examine o gráfico para avaliar se %defeituosos é distribuído aleatoriamente em tamanhos de amostra ou se um padrão está presente. Se os seus dados caírem aleatoriamente sobre a linha central, conclua que os dados seguem uma distribuição binomial.
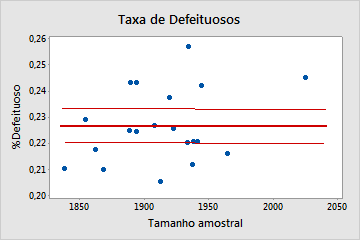
Binomial
Neste gráfico, os pontos são dispersos aleatoriamente ao redor da linha central. Você pode assumir que os dados seguem uma distribuição binomial. Portanto, os dados podem ser avaliados usando a análise de capacidade binomial.
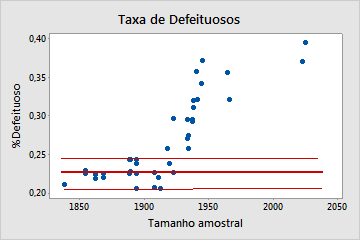
Não binomial
Neste gráfico, o padrão não é aleatório. Para tamanhos de amostra que são superiores a 1900, a taxa de %defeituosos aumenta conforme o tamanho da amostra aumenta. Este resultado indica uma correlação entre o tamanho da amostra e a porcentagem de defeituosos. Portanto, os dados não seguem uma distribuição binomial e não podem ser avaliados de forma confiável usando análise de capacidade binomial.
Etapa 3: Avalie a porcentagem de unidades defeituosas
Examine a estimativa e IC de %defeituosos
Utilize a média de %defeituosos dos dados de amostra para estimar a média de %defeituosos para o processo. Use o intervalo de confiança como uma margem de erro para a estimativa.
O intervalo de confiança oferece uma variedade de valores prováveis para o valor real do %defeituosos no seu processo (caso fosse possível coletar e analisar todos os itens que ele produz). A um nível de confiança de 95%, é possível ter 95% de confiança de que o %defeituosos real do processo esteja contido dentro do intervalo de confiança. Ou seja, se você coletar 100 amostras aleatórias de seu processo, você pode esperar que cerca de 95 das amostras produzam intervalos que contêm o valor real do %defeituosos.
O intervalo de confiança ajuda a avaliar a significância prática de seus resultados. Se você tiver um valor de %defeituosos máximo permitido que seja baseado no conhecimento de processo ou em padrões do setor, compare o limite de confiança superior com esse valor. Se o limite de confiança superior for menor que o valor de %defeituosos máximo permitido, é possível ter certeza que seu processo atende às especificações, mesmo levando-se em consideração a variabilidade de amostragem aleatória que afeta a estimativa.
| Estatísticas de Resumo | |
|---|---|
| (95,0% de confiança) | |
| %Defeituosos: | 0,39 |
| IC inferior: | 0,24 |
| IC superior: | 0,60 |
| Alvo: | 0,50 |
| PPM Def: | 3931 |
| IC inferior: | 2435 |
| IC superior: | 6003 |
| Processo Z: | 2,6579 |
| IC inferior: | 2,512 |
| IC superior: | 2,8155 |
Principais resultados: %defeituosos, IC
Os resultados para a análise de capacidade binomial incluem uma tabela de Estatísticas de Resumo, localizada na parte média inferior da saída. Nesta tabela de Estatísticas de Resumo simulada, o alvo (0,50%) indica o %defeituosos máximo permitida para o processo. O %defeituoso estimado é 0,39%, que é inferior ao %defeituosos máximo permitido. No entanto, o IC superior para %defeituosos é de 0,60%, o que excede o valor máximo permitido. Portanto, não é possível ter 95% de certeza de que o processo é capaz. Talvez seja necessário usar uma amostra maior ou reduzir a variabilidade do processo para obter um intervalo de confiança mais estreito para a estimativa do %defeituosos.
Determine se você tem dados suficientes para uma estimativa confiável
Use o Gráfico de %Defeituosos acumulado para determinar se você tem amostras suficientes para uma estimativa estável do %defeituosos.
Examine o %defeituosos para as amostras ordenadas por horário para ver como a estimativa muda conforme você coleta mais amostras. De maneira ideal, o %defeituosos estabiliza depois de várias amostras, como mostrado por um achatamento dos pontos representados graficamente ao longo da linha de %defeituosos médios.
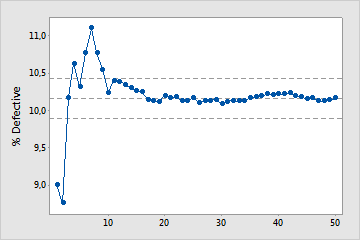
Amostras suficientes
Neste gráfico, %defeituosos estabiliza-se ao longo da linha de %defeituosos média. Portanto, o estudo inclui a capacidade de amostras suficientes para produzir uma estimativa estável e confiável de um %defeituosos.
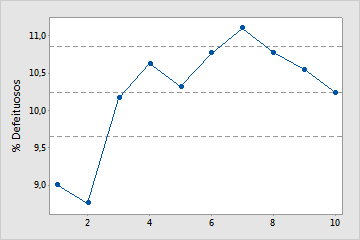
Sem amostras suficientes
Neste gráfico, %defeituosos não se estabilizar. Portanto, o estudo de capacidade não inclui amostras suficientes para estimar de forma confiável a média de %defeituosos.
