Os engenheiros de qualidade em uma empresa que fabrica pisos investigam as reclamações de clientes sobre deformação em seus produtos. Para assegurar a qualidade da produção, os engenheiros medem a deformação em 10 ladrilhos a cada dia útil durante 10 dias. O limite superior de especificação para a medição de empenamento é de 6 mm. Os engenheiros querem explorar diferentes opções para encontrar um método razoável para estimar a capacidade do processo.
- Abra os dados amostrais, DeformaçãoLadrilho.MWX.
- Escolha .
- Em Coluna única, digite Deformação.
- Em Tamanho do subgrupo, insira 10.
- Em Espec superior, insira 6.
- Selecione OK.
Interpretar os resultados
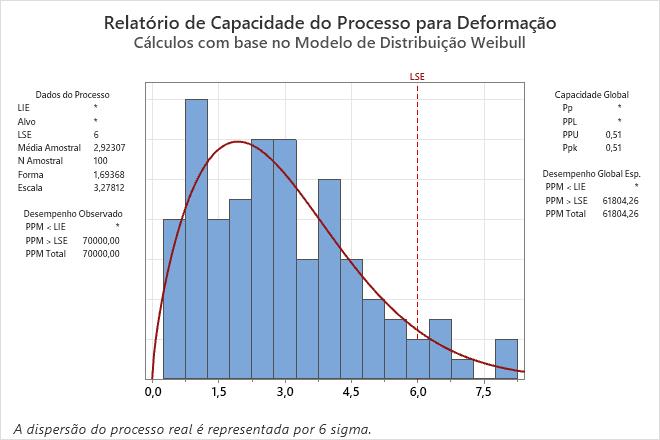
A análise exibe um relatório de capacidade para o primeiro método que fornece um ajuste razoável. Para o empenamento das telhas, os resultados utilizam uma distribuição Weibull.
Para esses dados, as medidas na cauda direita do histograma parecem estar acima do limite superior de especificação. Portanto, o empenamento das telhas frequentemente excede o limite superior de especificação de 6 mm. O PPM observado > USL indica que 70.000 de cada milhão de blocos estão acima do limite superior de especificação. O Ppk global esperado é de 0,51, o que é menor do que o valor geralmente aceito pelas diretrizes do setor de 1,33. Portanto, os engenheiros concluem que o processo não é capaz e não atende às necessidades dos clientes.
A tabela de distribuição dos resultados mostra a ordem de avaliação dos métodos. Na primeira linha, a conclusão para o teste de Anderson-Darling é que os dados não seguem uma distribuição normal ao nível de significância de 0,05, pois o valor de p é menor que 0,05. Na segunda linha, a conclusão para o teste de Anderson-Darling é que a distribuição de Weibull é um ajuste razoável aos dados, pois o valor de p é maior que 0,05. Os resultados de capacidade são para a distribuição Weibull porque a distribuição Weibull é o primeiro método na lista que fornece um ajuste razoável.
Os engenheiros usam o conhecimento do processo para considerar se a distribuição Weibull é uma seleção razoável. Por exemplo, a distribuição Weibull tem um limite em 0. Nos dados, 0 é um limite que representa um bloco não distorcido.
Resultados da distribuição automatizada de capacidades: Deformação
| Distribuição | Local | Escala | Limite | Forma | P | Ppk | Cpk |
|---|---|---|---|---|---|---|---|
| Normal | 2,9231 | 1,7860 | 0,0100421 | 0,5743 | 0,5838 | ||
| Weibull* | 3,2781 | 1,6937 | >0,25 | 0,5133 | |||
| Lognormal | 0,8443 | 0,7444 | <0,005 | 0,4242 | |||
| Menor Valor Extremo | 3,8641 | 1,9924 | <0,01 | 0,5362 | |||
| Maior Valor Extremo | 2,0958 | 1,4196 | 0,212835 | 0,5130 | |||
| Gama | 1,2477 | 2,3428 | 0,238337 | 0,4851 | |||
| Logística | 2,7959 | 1,0162 | 0,0127347 | 0,5799 | |||
| Loglogística | 0,9097 | 0,4217 | <0,005 | 0,4090 | |||
| Exponencial | 2,9231 | <0,0025 | 0,3780 | ||||
| Weibull de 3 Parâmetros | 2,9969 | 0,2099 | 1,5049 | 0,467097 | 0,4980 | ||
| Lognormal de 3 Parâmetros | 1,3788 | 0,4184 | -1,4002 | 0,4961 | |||
| Gama de 3 Parâmetros | 1,2314 | -0,0197 | 2,3898 | 0,4864 | |||
| Loglogística de 3 Parâmetros | 1,3043 | 0,2700 | -1,0940 | 0,4656 | |||
| Exponencial de 2 Parâmetros | 2,6679 | 0,2552 | <0,01 | 0,3982 | |||
| Transformação de Box-Cox | 1,6237 | 0,5380 | 0,574337 | 0,5116 | 0,5214 | ||
| Transformação de Johnson | 0,0112 | 0,9949 | 0,798895 | 0,4959 | |||
| Não-paramétrico | 0,6187 |
