Uma distribuição de amostragem descreve a probabilidade de se obter todos os valores possíveis de uma estatística em uma amostra aleatória de uma população; em outras palavras, qual proporção de todas as amostras aleatórias desse tamanho fornecerão esse valor. Bootstrapping é um método que estima a distribuição de amostragem que coleta várias amostras com reposição de uma amostra aleatória única. Essas amostras repetidas são chamadas reamostras. Cada reamostra é do mesmo tamanho da amostra original.
A amostra original representa a população da qual ela foi coletada. Portanto, as reamostras desta amostra original representam o que nós obteríamos se tirássemos várias amostras da população. A distribuição por bootstrap da estatística, baseada nas reamostras, representa a distribuição de amostragem da estatística.
Por exemplo, você quer estimar a distribuição de amostragem da proporção de M&Ms azuis. Você abre um pacote ao acaso e determina que há 102 M&Ms, dos quais 23 (22,5%) são azuis. A amostragem repetida com reposição desta amostra original simula o perfil da população. Para fazer uma reamostra, um M&M é selecionado aleatoriamente da amostra original, a cor é registrada e o M&M é colocado de volta na amostra. Isto é feito 102 vezes (o tamanho da amostra original) para completar uma reamostra única. O gráfico de barras a seguir representa uma única amostra por bootstrap retirada da amostra original.
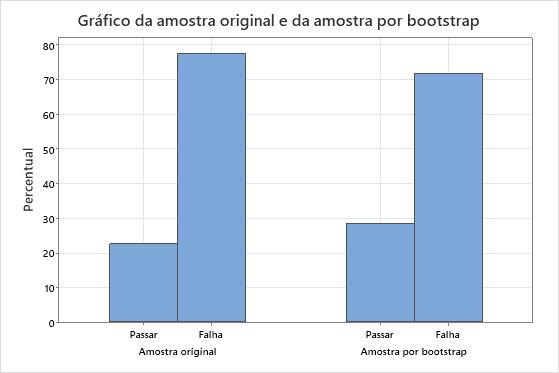
Dado que a reamostra é realizada por meio de amostragem com reposição, a proporção da amostra por bootstrap não será necessariamente igual à proporção original. Este gráfico de barras mostra que a amostra original tem aproximadamente 22,5% de M&Ms azuis, enquanto a amostra por bootstrap tem aproximadamente 28,4% de M&Ms azuis. Para criar uma distribuição por bootstrap, você deve sortear várias reamostras. O histograma a seguir mostra a distribuição por bootstrap para 1.000 reamostras do pacote original de M&Ms.
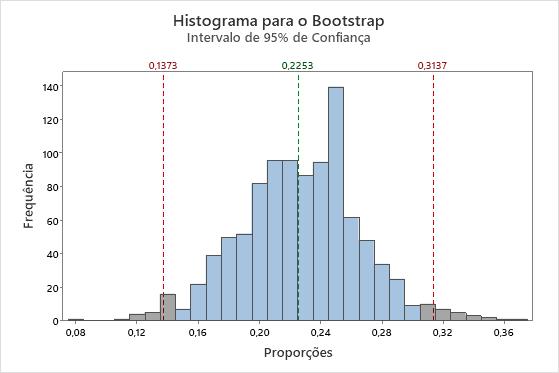
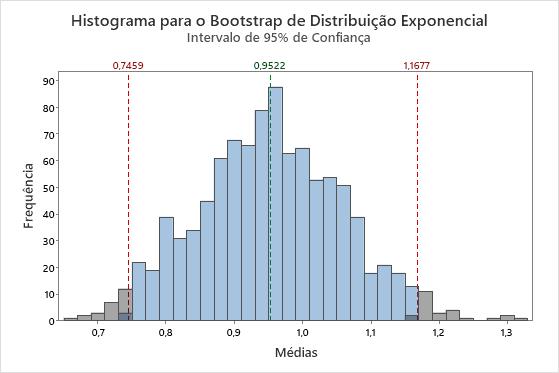
A distribuição por bootstrap está centrada a aproximadamente 22,5%, o que é uma estimativa da proporção populacional. As linhas de referência vermelhas representam o intervalo de confiança a 95%. O meio dos 95% dos valores da distribuição por bootstrapping fornecem um intervalo de confiança a 95% para a proporção da população de M&Ms azuis. Neste exemplo, você pode ter 95% de confiança quanto à proporção da população de M&Ms azuis estar entre 13,7% e 31,4% (aproximadamente).
Bootstrapping e o teorema central do limite
O teorema central do limite é um teorema fundamental da probabilidade e estatística. O teorema afirma que a distribuição de 
, que é a média de uma amostra aleatória de uma população com variância finita, é aproximadamente normalmente distribuída quando o tamanho amostral é grande, independentemente da forma da distribuição da população. O bootstrapping pode ser usado para entender de maneira fácil como o teorema central do limite funciona. Considere que os dados vêm de uma distribuição exponencial.
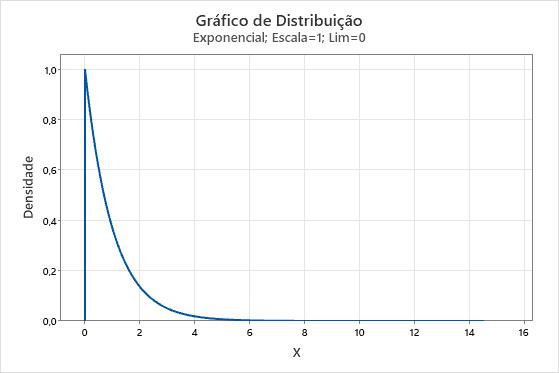
É evidente que os dados não são normais. Mas nós tomaremos uma amostra de 50 observações e criaremos uma distribuição por bootstrap das médias de 10 reamostras.
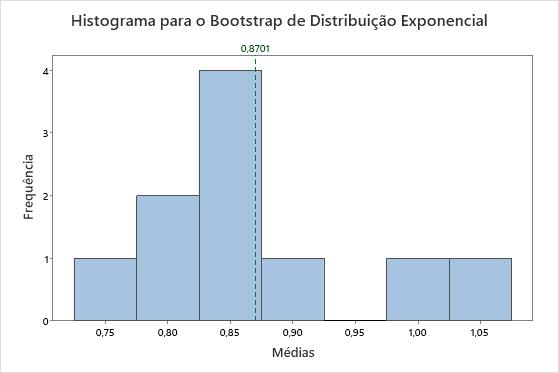
A distribuição das médias é muito diferente da distribuição exponencial. Ela é mais assemelhada com a distribuição normal. Essa semelhança aumenta conforme o número de reamostras aumenta. Com 1.000 reamostras, a distribuição da média das reamostras é aproximadamente normal.
