O que é distribuição de Poisson?
A distribuição de Poisson é especificada por um parâmetro: lambda (λ). Este parâmetro é igual à média e à variância. Conforme lambda aumenta para valores suficientemente grandes, a distribuição normal (λ, λ) pode ser usada para aproximar a distribuição de Poisson.
Use a distribuição de Poisson para descrever o número de vezes que um evento ocorre em um espaço de observação finito. Por exemplo, uma distribuição de Poisson pode descrever o número de defeitos no sistema mecânico de um avião ou o número de chamadas para uma central de atendimento por hora. A distribuição de Poisson é frequentemente usada no controle de qualidade, em estudos de confiabilidade/sobrevivência e seguro.
- Os dados são contagens de eventos (inteiros não-negativos com nenhum limite superior).
- Todos os eventos são independentes.
- A taxa média não muda sobre o período de interesse.
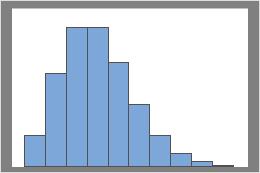
Lambda = 3
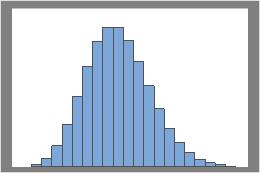
Lambda = 10
O que é taxa de ocorrência?
A taxa de ocorrência é igual à média (λ) dividida pela dimensão do seu espaço de observação. É útil para comparar contagens de Poisson coletadas em diferentes espaços de observação. Por exemplo, a central telefônica A recebe 50 chamadas telefônicas em 5 horas, e a central telefônica B recebe 80 chamadas em 10 horas. Você não pode comparar diretamente esses valores porque seus espaços de observação são diferentes. Você deve calcular a taxa de ocorrência para comparar essas contagens. A taxa para a central telefônica A é (50 chamadas / 5 horas) = 10 chamadas/hora. A taxa da central telefônica B é (80 chamadas / 10 horas) = 8 chamadas/hora.
As diferenças entre a distribuição de Poisson e a distribuição binomial
A distribuição de Poisson é similar à distribuição binomial porque ambas modelam contagens de eventos. Contudo, dentro do seu espaço de observação finito, a distribuição de Poisson não coloca nenhum limite superior nesta contagem: uma mesa telefônica poderia receber um número ilimitado de chamadas em um dia e não violar os requisitos de distribuição de Poisson. Por outro lado, a distribuição binomial define um limite superior na contagem: o número de eventos que você observa não pode ser maior do que o número de ensaios que você realiza.
