O que é uma distribuição hipergeométrica?
A distribuição hipergeométrica é uma distribuição discreta que modela o número de eventos em um tamanho amostral fixo quando você conhece o número total de itens da população de onde vem a amostra. Cada item da amostra tem dois resultados possíveis (um evento ou um não-evento). As amostras são sem substituição, portanto, cada item da amostra é diferente. Quando um item é escolhido da população, ele não pode ser escolhido novamente. Portanto, a chance de um determinado item ser selecionado aumenta em cada ensaio, supondo-se que ele ainda não tenha sido selecionado.
Use a distribuição hipergeométrica para amostras extraídas de populações relativamente pequenas, sem substituição. Por exemplo, a distribuição hipergeométrica é usada no teste exato de Fisher para testar a diferença entre duas proporções e na amostragem de aceitação por atributos para a amostragem de um lote isolado de tamanho finito.
A distribuição hipergeométrica é definida por 3 parâmetros: tamanho da população, contagem de evento na população e tamanho amostral.
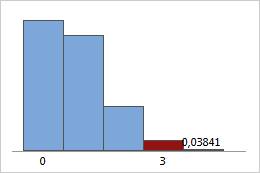
Exemplo de cálculo de probabilidades hipergeométrica
Suponha que há dez carros disponíveis para você para test drive (N = 10), e cinco dos carros têm motores turbo (x = 5). Se você testar três dos carros (n = 3), qual é a probabilidade de que dois dos três carros que você dirige tenham motores turbo?
- Selecione .
- Selecione Probabilidade.
- Em Tamanho da população (N), insira 10. Em Contagem de eventos na população (M), insira 5. Em Tamanho amostral (n), insira 3.
- Escolha Constante de entrada e insira 2.
- Clique em OK.
A probabilidade de você selecionar aleatoriamente exatamente dois carros com motores turbo quando você testar três dos dez carros em que está interessado é 41,67%.
A diferença entre o hipergeométrico e distribuição binomial
Ambas as distribuições hipergeométrica e a binomial descrevem o número de vezes que um evento ocorre em um número de dados fixo de ensaios. Para a distribuição binomial, a probabilidade é a mesma para todos os ensaios. Para a distribuição hipergeométrica, cada ensaio muda a probabilidade de cada ensaio subsequente porque não há substituição.
Utilize a distribuição binomial com populações tão grandes que o resultado de um ensaio exerça quase nenhum efeito sobre a probabilidade de que o próximo resultado seja um evento ou não evento. Por exemplo, numa população de 100.000 pessoas, 53.000 têm sangue O+. A probabilidade de que a primeira pessoa selecionada aleatoriamente em uma amostra de sangue tenha O+ é de 0,530 mil. Se a primeira pessoa em uma amostra tiver sangue O+, então a probabilidade de que a segunda pessoa tenha sangue O+ é 0,529995. A diferença entre estas probabilidades é pequena o suficiente para ignorar para a maioria das aplicações.
Utilize a distribuição hipergeométrica com populações tão pequenas que o resultado de um ensaio exerça um grande efeito sobre a probabilidade de que o próximo resultado seja um evento ou não evento. Por exemplo, numa população de 10 pessoas, 7 têm sangue O+. A probabilidade de que a primeira pessoa selecionada aleatoriamente em uma amostra tenha sangue O+ é 0,70000. Se a primeira pessoa na amostra tiver sangue O+, então a probabilidade de que a segunda pessoa tenha sangue O+ é 0,66667. A diferença pode aumentar à medida que o tamanho da amostra aumenta. A diferença entre estas probabilidades é grande demais para ignorar para muitas aplicações.
