O que é a função de densidade de probabilidade (FDP)?
A função de densidade de probabilidade ajuda a identificar regiões de probabilidades superiores e inferiores para os valores de uma variável aleatória.
Exemplo de uma FDP discreta
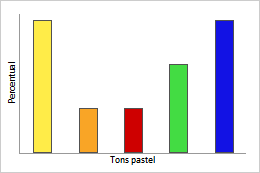
FDP discreta
Este gráfico de barras exibe a FDP para a cor doces. Cada barra representa a probabilidade dos doces daquela cor expressos como uma porcentagem.
Exemplo de uma FDP contínua
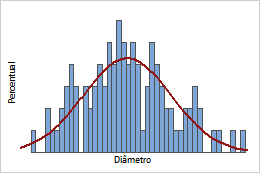
FDP contínua
A curva é a FDP para o diâmetro da rolha. Use a FDP para identificar as áreas de probabilidades superiores e inferiores para os valores de uma variável aleatória. Por exemplo, apenas uma pequena porcentagem das rolhas (1%) tem um diâmetro inferior a 2,8 cm.
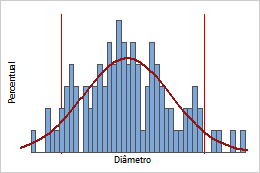
FDP contínua com limites de especificação
Se os limites de especificação para diâmetro de rolha forem de 2,85 cm a 3,15 cm, o FDP pode indicar valores de densidade de probabilidade de todas as rolhas deste processo que atendam às especificações.
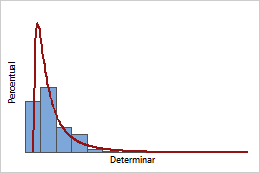
FDP lognormal
Como uma garrafa de vinho ocasionalmente requer uma quantidade incomum de força para a retirada da rolha, as medidas desta força muitas vezes seguem uma distribuição com uma longa cauda direita como a distribuição lognormal.
