Exemplo de uso de ICDF para determinar os períodos de garantia
Por exemplo, uma fabricante de aparelhos investiga tempos de falha para o elemento de aquecimento dentro de suas torradeiras. Ele quer determinar a hora em que proporções específicas de elementos aquecedores irão falhar, de forma ele possa definir o período de garantia. Os tempos de falha do elemento de aquecimento seguem uma distribuição normal com uma média de 1000 horas e um desvio padrão de 300 horas. A função densidade de probabilidade (PDF) ajuda a identificar regiões com probabilidades de falha maiores e menores. A FDA inversa dá o tempo de falha correspondente para cada probabilidade acumulada.
Use a FDA inversa para estimar o tempo no qual 5% dos elementos de aquecimento irão falhar, os tempos entre os quais 95% de todos os elementos de aquecimento irão falhar ou o tempo no qual somente 5% dos elementos de aquecimento permanecem. A FDA inversa para probabilidades acumuladas específicas é igual ao tempo de falha no lado direito da área sombreada sob a curva de FDP.
Determine o momento em que 5% falhará
- Escolha .
- Escolha Probabilidade acumulada inversa. Em Média, insira 1000. Em Desvio padrão, insira 300. Em Constante de entrada, insira 0,05.
- Clique em OK.
O tempo em que prevê-se que 5% dos elementos de aquecimento falhem é a FDA inversa de 0,05 ou 506,544 horas.
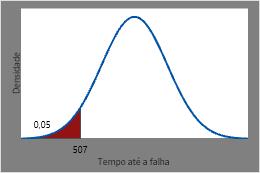
Este gráfico mostra a FDA inversa.
Determinar os momentos entre as quais 95% falharão
- Escolha .
- Escolha Probabilidade acumulada inversa. Em Média, insira 1000. Em Desvio padrão, insira 300. Em Constante de entrada, insira 0,025. Clique em OK.
O tempo em que prevê-se que 2,5% dos elementos de aquecimento falhem é a FDA inversa de 0,025 ou 412 horas.
- Repita o passo 2, mas insira 0,975 em vez de 0,025. Clique em OK.O tempo em que prevê-se que 97,5% dos elementos de aquecimento falhem é a FDA inversa de 0,975 ou 1588 horas.
Portanto, os tempos entre os quais é previsto que 95% de todos os elementos de aquecimento falhem é a FDA inversa de 0,025 e a FDA inversa de 0,975 ou 412 horas e 1588 horas.
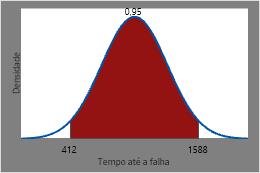
Este gráfico mostra a FDA inversa.
Determine o tempo em que 5% sobreviverão
- Escolha .
- Escolha Probabilidade acumulada inversa. Em Média, insira 1000. Em Desvio padrão, insira 300. Em Constante de entrada, insira 0,95.
- Clique em OK.
O tempo em que prevê-se que 5% dos elementos de aquecimento permaneçam é a FDA inversa de 0,95 ou 1493 horas.
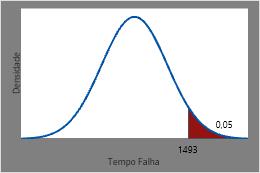
Este gráfico mostra a FDA inversa.
Exemplo de uso da FDA e da ICDF com a distribuição hipergeométrica
Ao tentar determinar a probabilidade acumulada inversa de uma distribuição discreta, a saída contém dois conjuntos de colunas.
Suponha que você tenha a probabilidade acumulada inversa de uma proporção, p. O primeiro conjunto de colunas na saída lista os maiores x, tal que P (X ≤ x) ≤ p. O segundo conjunto de colunas lista os menores x tal que P (X ≤ x) ≥ p.
Calcule a probabilidade acumulada de uma distribuição hipergeométrica
- Na coluna C1, digite 0 1 2.
C1 0 1 2 - Escolha .
- Escolha Probabilidade acumulada.
- Em Tamanho da população (N), tipo 20000.
- Em Contagem de eventos na população (M), tipo 2000.
- Em Tamanho amostral (n), tipo 20.
- Escolha Coluna de entrada e insira C1. Clique em OK.
Função Distribuição Acumulada
- P(X ≤ 0) = 0,121448. A probabilidade de obter 0 defeitos é de aproximadamente 12%.
- P(X ≤ 1) = 0,391619. A probabilidade de obter 0, ou 1 defeito é de aproximadamente 39%.
- P(X ≤ 2) = 0,676941. A probabilidade de obter 0, 1, ou 2 defeitos é de aproximadamente 68%.
Calcule a probabilidade acumulada de uma distribuição inversa hipergeométrica
Agora que você conhece as probabilidades acumuladas associadas com o número de defeitos, calcula a probabilidade acumulada inversa.
Suponha que você queira calcular o número de defeitos, x, tal que a probabilidade acumulada, p, seja de 0,50. A partir dos resultados anteriores, você sabe que P (X ≤ 1) = 0,391619 e P (X ≤ 2) = 0,676941. Como a distribuição hipergeométrica é discreta, o número de defeitos não pode estar entre 1 e 2. Em outras palavras, você pode ter 1 ou 2 defeitos, mas não 1,4 defeitos. Portanto, se você escolher Constante de entrada e inserir 0,50, o Minitab calcula ambas as probabilidades na saída, como mostrado no exemplo a seguir:
- Escolha .
- Escolha Probabilidade acumulada inversa.
- Em Tamanho da população (N), tipo 20000.
- Em Contagem de eventos na população (M), tipo 2000.
- Em Tamanho amostral (n), tipo 20.
- Escolha Constante de entrada, e digite 0,50. Clique em OK.
Função Distribuição Acumulada Inversa
A primeira probabilidade indica um valor de x tal que P(X ≤ x) < p and the second probability indicates the smallest x such that P(X ≤ x) ≥ p. In this example, the first probability shows the largest number of defectives, x = 2, such that P(X ≤ 2) <0.5 and the 2nd mostra o menor número de deficientes, x = 3, tal que P(X ≤ 3) ≥ 0,5.
Use a ICDF para calcular os valores essenciais
Você pode usar o Minitab para calcular um valor crítico para um teste de hipóteses, em vez de olhar em uma tabela.
Suponha que você realize um teste de qui-quadrado com α = 0,02 e 12 graus de liberdade. Qual é o valor crítico correspondente? Um α=0,02 corresponde a um valor de probabilidade acumulada de 1 - 0,02 = 0,98.
- Escolha .
- Escolha Probabilidade acumulada inversa.
- Em Graus de liberdade, insira 12.
- Escolha Constante de entrada e insira 0,98.
- Clique em OK.
O Minitab exibe o valor crítico, 24,054. Para o teste qui-quadrado, se a estatística do teste for maior que o valor crítico, pode-se concluir que há evidências estatísticas para rejeitar a hipótese nula.
Observação
Este exemplo utiliza a distribuição qui-quadrado. No entanto, você deve seguir estas mesmas etapas para qualquer distribuição selecionada.
