Neste tópico
- Função densidade de probabilidade
- Função distribuição acumulada
- Probabilidade acumulada inversa
- Distribuição Beta
- Distribuição binomial
- Distribuição Cauchy
- Distribuição Qui-Quadrado
- Distribuição discreta
- Distribuição exponencial
- Distribuição F
- Distribuição gama
- Distribuição geométrica
- Distribuição Hipergeométrica
- Distribuição inteira
- Distribuição normal
- Distribuição de Laplace
- Distribuição do maior valor extremo
- Distribuição logística
- Distribuição loglogística
- Distribuição lognormal
- Distribuição binomial negativa
- Distribuição de Poisson
- Distribuição do menor valor extremo
- Distribuição-t
- Distribuição triangular
- Distribuição uniforme
- Distribuição Weibull
Função densidade de probabilidade
- Para distribuições contínuas, a probabilidade de que X tenha os valores em um intervalo (a, b) é exatamente a área sob a sua FDP no intervalo (a, b).
- Para as distribuições discretas, a probabilidade de que X tenha os valores em um intervalo (a, b) é exatamente a soma das FDP (também chamadas de função de densidade de probabilidade) dos possíveis valores discretos de X em (a, b).
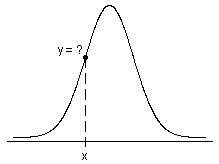
Função distribuição acumulada
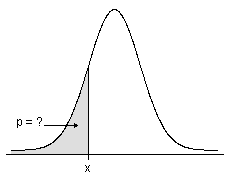
- Para distribuições contínuas, a FDA dá a área sob a função densidade de probabilidade, até o valor de x que você especificar.
- Para distribuições discretas, a FDA dá a probabilidade acumulada para os valores de x que você especificar.
Probabilidade acumulada inversa
Para um número p no intervalo fechado [0,1], a função de distribuição acumulada inversa (ICDF) de uma variável aleatória X determina, sempre que possível, um valor x de modo que a probabilidade de X ≤ x seja maior ou igual a p .
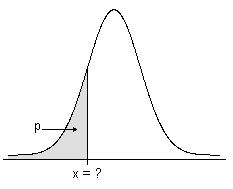
- A ICDF para distribuições contínuas
-
A ICDF é o valor que está associado com uma área sob a função densidade de probabilidade. A ICDF é a inversa da função distribuição acumulada (FDA), que é a área associada a um valor.
Para todas as distribuições contínuas, existe a ICDF e ela é única se 0 < p < 1.
- Quando a função de densidade de probabilidade (FDP) é positiva para toda a linha número real (por exemplo, uma FDP normal), a ICDF não é definida por qualquer p = 0 ou p = 1.
- Quando a FDP for positiva para todos os valores que são maiores do que algum valor (por exemplo, a FDP do qui-quadrado), a ICDF é definida para p = 0, mas não para P = 1.
- Quando a FDP é positiva apenas em um intervalo (por exemplo, a FDP uniforme), a ICDF é definida para p = 0 e p = 1.
- Quando a ICDF não está definida, o Minitab retorna um valor faltante (*) para o resultado.
- A ICDF para distribuições discretas
- A ICDF é mais complicada para distribuições discretas do que é para distribuições contínuas. Ao calcular a FDA para uma binomial com, por exemplo, n = 5 e p = 0,4, não existe um valor x tal que a FDA seja de 0,5. Para x = 1, a FDA é 0,3370. Para x = 2, a FDA aumenta para 0,6826.
Distribuição Beta
A distribuição beta é normalmente usada para representar processos com limites naturais inferiores e superiores.
Fórmula
A função de densidade de probabilidade (FDP) é:

Notação
| Termo | Descrição |
|---|---|
| α | parâmetro de forma 1 |
| β | parâmetro de forma 2 |
| Γ | função gama |
| a | limite inferior |
| b | limite superior |
Quando a = 0, b = 1,
o FDP é:
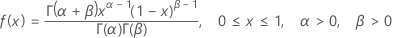


Distribuição binomial
A distribuição binomial é usada para representar o número de eventos que ocorrem dentro de n tentativas independentes. Os valores possíveis são números inteiros de zero a n.
Fórmula
média = np
variância = np(1 – p)
A função de massa de probabilidade (FMP) é:
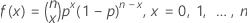
Onde  é igual a
é igual a  .
.
Em geral, é possível calcular k! como 
Notação
| Termo | Descrição |
|---|---|
| n | número de ensaios |
| x | número de eventos |
| p | probabilidade de evento |
Distribuição Cauchy
A distribuição Cauchy é simétrica em torno de zero, mas as caudas se aproximam de zero menos rapidamente do que aqueles da distribuição normal.
Fórmula
A função de densidade de probabilidade (FDP) é:
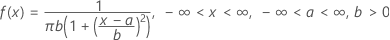
Notação
| Termo | Descrição |
|---|---|
| a | parâmetro de localização |
| b | parâmetro de escala |
| π | Pi (~3,142) |
Observação
Se você não especificar valores, o Minitab usa a = 0 e b = 1.
Distribuição Qui-Quadrado
Se X tiver uma distribuição normal padrão, X2 tem uma distribuição do qui-quadrado com um grau de liberdade, permitindo que ele seja uma distribuição de amostragem utilizada.
A soma de n variáveis X2 independentes (onde X tem uma distribuição normal padrão) tem uma distribuição qui-quadrado com n graus de liberdade. A forma da distribuição do qui-quadrado depende do número de graus de liberdade.
Fórmula
A função de densidade de probabilidade (FDP) é:
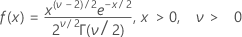
médoa = v
variância = 2v
Notação
| Termo | Descrição |
|---|---|
| ν | graus de liberdade |
| Γ | função gama |
| e | base do logaritmo natural |
Distribuição discreta
A distribuição discreta é aquela que você mesmo define. Por exemplo, suponha que você esteja interessado em uma distribuição composta por três valores -1, 0, 1, com probabilidades de 0,2, 0,5 e 0,3, respectivamente. Se você digitar os valores em colunas de uma worksheet, pode usar essas colunas para gerar dados aleatórios ou para calcular probabilidades.
| Valor | Prob |
|---|---|
| −1 | 0,2 |
| 0 | 0,5 |
| 1 | 0,3 |
Distribuição exponencial
A distribuição exponencial pode ser utilizada para modelar o tempo entre falhas, como quando as unidades possuem uma taxa constante e instantânea de falha (função de risco). A distribuição exponencial é um caso especial da distribuição Weibull e da distribuição gama.
Fórmula
A função de densidade de probabilidade (FDP) é:
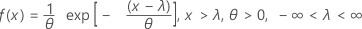
A função de distribuição acumulada (FDA) é:

média = θ + λ
variância = θ2
Notação
| Termo | Descrição |
|---|---|
| θ | parâmetro de escala |
| λ | parâmetro de limite |
| exp | base do logaritmo natural |
Observação
Algumas referências usam 1 / θ como um parâmetro.
Distribuição F
A distribuição F também é conhecida como a distribuição de variância-proporção e tem dois tipos de graus de liberdade: graus de liberdade do numerador e denominador graus de liberdade. Ela é uma distribuição de proporção de duas variáveis aleatórias independentes com distribuição qui-quadrado, cada uma dividida por seus graus de liberdade.
Fórmula
A função de densidade de probabilidade (FDP) é:
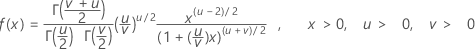

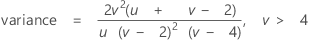
Notação
| Termo | Descrição |
|---|---|
| Γ | função gama |
| u | graus de liberdade do numerador |
| v | graus de liberdade do denominador |
Distribuição gama
A distribuição gama é normalmente usada para modelar dados positivamente assimétricos.
Fórmula
A função de densidade de probabilidade (FDP) é:

média = ab + θ
variância = ab2
Notação
| Termo | Descrição |
|---|---|
| a | parâmetro de forma (quando a = 1 o FDP de gama for igual ao FDP exponencial) |
| b | parâmetro de escala |
| θ | parâmetro de limite |
| Γ | função gama |
| e | base do logaritmo natural |
Observação
Algumas referências usam 1/ b como um parâmetro.
Distribuição geométrica
A distribuição geométrica discreta se aplica a uma sequência de experimentos independentes de Bernoulli com um evento de interesse que tem probabilidade p.
Fórmula
Se a variável aleatória X for o número total de ensaios necessários para produzir um evento com a probabilidade p, a função de massa de probabilidade (FMP) de X é dada por:

e X apresenta as seguintes propriedades:


Se a variável aleatória Y for o número de não eventos que ocorrem antes de o primeiro evento com a probabilidade p ser observado, a função de massa de probabilidade (FMP) de Y é dada por:

e Y apresentações das propriedades a seguir:


Notação
| Termo | Descrição |
|---|---|
| X | número total de ensaios necessários para produzir um evento, Y + 1 |
| Y | número de não eventos que ocorrem antes do primeiro evento |
| p | probabilidade de ocorrência de um evento em cada ensaio |
Distribuição Hipergeométrica
A distribuição hipergeométrica é usada para amostras extraídas de populações relativamente pequenas, sem substituição. Por exemplo, você tem uma remessa de N televisores, onde N1 são bons (sucessos) e N2 são defeituosos (falha). Se você amostrar n televisores de N aleatoriamente, sem substituição, pode encontrar a probabilidade de que exatamente x dos n televisores estão bons.
Fórmula
A função de massa de probabilidade (FMP) é:
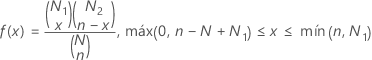


Notação
| Termo | Descrição |
|---|---|
| N | N1 + N2 = tamanho da população |
| N1 | número de eventos na população |
| N2 | número de não eventos na população |
| n | tamanho amostral |
| x | número de eventos na amostra |
Distribuição inteira
A distribuição inteira é uma distribuição uniforme discreta em um conjunto de números inteiros. Cada inteiro tem igual probabilidade de ocorrência.
Distribuição normal
A distribuição normal (também chamada distribuição de Gauss), é a distribuição estatística mais utilizada por causa dos muitos processos físicos, biológicos e sociais que pode modelar.
Fórmula
A função de densidade de probabilidade (FDP) é:
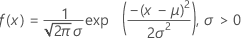
A função de distribuição acumulada (FDA) é:
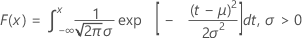
média = μ
variância = σ 2
desvio padrão = σ
Notação
| Termo | Descrição |
|---|---|
| exp | base do logaritmo natural |
| π | Pi (~3,142) |
Distribuição de Laplace
A distribuição de Laplace é utilizada quando a distribuição de dados tiver mais picos do que a distribuição normal.
Fórmula
A função de densidade de probabilidade (FDP) é:
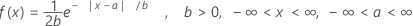
média = a
variância = 2b2
Notação
| Termo | Descrição |
|---|---|
| a | parâmetro de localização |
| b | parâmetro de escala |
| e | base do logaritmo natural |
Distribuição do maior valor extremo
Use a distribuição do maior valor extremo para modelar o maior valor de uma distribuição. Se você tiver uma sequência de distribuições exponenciais, e X(n) for o máximo do primeiro n, X(n) – ln(n) converge em distribuição para a distribuição de maior valor extremo. Assim, para grandes valores de n, a distribuição de maior valor extremo é uma boa aproximação para a distribuição de X(n) – ln(n).
Fórmula
A função de densidade de probabilidade (FDP) é:

A função de distribuição acumulada (FDA) é:

média = μ + γσ
variância = π 2 σ 2 / 6
Notação
| Termo | Descrição |
|---|---|
| σ | parâmetro de escala |
| μ | parâmetro de localização |
| γ | Constante de Euler (~0,57722) |
Distribuição logística
É uma distribuição contínua que é simétrica, semelhante à distribuição normal, mas com caudas mais pesadas.
Fórmula
A função de densidade de probabilidade (FDP) é:
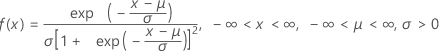
A função de distribuição acumulada (FDA) é:
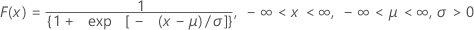
média = μ
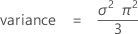
Notação
| Termo | Descrição |
|---|---|
| μ | parâmetro de localização |
| σ | parâmetro de escala |
Distribuição loglogística
Uma variável x tem uma distribuição loglogística com limite λ se Y = log (x – λ) tiver uma distribuição logística.
Fórmula
A função de densidade de probabilidade (FDP) é:
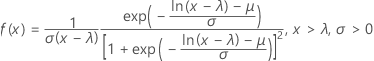
A função de distribuição acumulada (FDA) é:

quando σ < 1:

quando σ < 1/2:
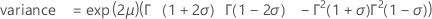
Notação
| Termo | Descrição |
|---|---|
| μ | parâmetro de localização |
| σ | parâmetro de escala |
| λ | parâmetro de limite |
| Γ | função gama |
| exp | base do logaritmo natural |
Distribuição lognormal
Uma variável x tem uma distribuição lognormal se log(x – λ ) tiver uma distribuição normal.
Fórmula
A função de densidade de probabilidade (FDP) é:

A função de distribuição acumulada (FDA) é:



Notação
| Termo | Descrição |
|---|---|
| μ | parâmetro de localização |
| σ | parâmetro de escala |
| λ | parâmetro de limite |
| π | Pi (~3,142) |
Distribuição binomial negativa
A distribuição binomial negativa discreta se aplica a uma série de experimentos de Bernoulli com um evento de interesse que tem probabilidade p.
Fórmula



Se a variável aleatória Y é o número de não eventos que ocorrem antes de observar os eventos r, que têm cada um a probabilidade p, a função de massa de probabilidade (FMP) de Y é dada por:
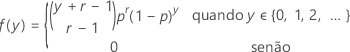
e Y apresentações das propriedades a seguir:


Observação
Esta distribuição binomial negativa também é conhecida como distribuição de Pascal.
Notação
| Termo | Descrição |
|---|---|
| X | Y + r |
| r | número de eventos |
| p | probabilidade de um evento |
Distribuição de Poisson
A distribuição de Poisson é uma distribuição discreta que modela o número de eventos baseados em uma taxa constante de ocorrência. A distribuição de Poisson pode ser usada como uma aproximação ao binomial quando o número de ensaios independentes é grande a probabilidade de sucesso é pequena.
Fórmula
A função de massa de probabilidade (FMP) é:
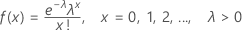
média = λ
variância = λ
Notação
| Termo | Descrição |
|---|---|
| e | base do logaritmo natural |
Distribuição do menor valor extremo
Use a distribuição do menor valor extremo para modelar o menor valor de uma distribuição. Se Y segue uma distribuição Weibull, o log(Y) segue a distribuição de menor valor extremo.
Fórmula
A função de densidade de probabilidade (FDP) é:
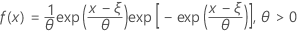
A função de distribuição acumulada (FDA) é:



Notação
| Termo | Descrição |
|---|---|
| ξ | parâmetro de localização |
| θ | parâmetro de escala |
| e | base do logaritmo natural |
| v | Constante de Euler (~0,57722) |
Distribuição-t
- Criar intervalos de confiança da média da população de uma distribuição normal quando a variância for desconhecida.
- Determinar se duas médias amostrais de populações normais com variâncias desconhecidas, porém iguais, são significativamente diferentes.
- Os testes da significância para os coeficientes de regressão.
Fórmula
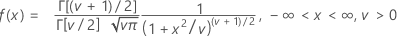
média = 0, quando ν > 0

Notação
| Termo | Descrição |
|---|---|
| Γ | função gama |
| v | graus de liberdade |
| π | Pi (~3,142) |
Distribuição triangular
O FDP da distribuição triangular tem uma forma triangular.
Fórmula
A função de densidade de probabilidade (FDP) é:
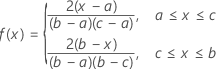
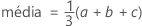
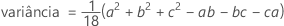
Notação
| Termo | Descrição |
|---|---|
| a | ponto de extremidade inferior |
| b | ponto de extremidade superior |
| c | modo (local onde o FDP entra em pico) |
Distribuição uniforme
A distribuição uniforme caracteriza dados sobre um intervalo uniforme, com a como o menor valor e b como o maior valor.
Fórmula
A função de densidade de probabilidade (FDP) é:



Notação
| Termo | Descrição |
|---|---|
| a | ponto de extremidade inferior |
| b | ponto de extremidade superior |
Distribuição Weibull
A distribuição Weibull é útil para modelar os tempos de falha do produto.
Fórmula
A função de densidade de probabilidade (FDP) é:
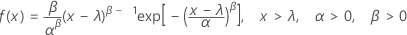
A função de distribuição acumulada (FDA) é:

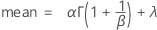
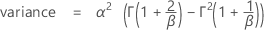
Notação
| Termo | Descrição |
|---|---|
| α | parâmetro de escala |
| β | parâmetro de forma, quando β = 1 o FDP de Weibull é for igual ao FDP exponencial |
| λ | parâmetro de limite |
| Γ | função gama |
| exp | base do logaritmo natural |
Observação
Algumas referências usam 1/α como um parâmetro.
