Neste tópico
Média
Uma medida tipicamente utilizada do centro de um grupo de números. A média é também chamada de a média. Ela é a soma de todas as observações dividida pelo número de observações (não faltantes).
Fórmula
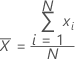
Notação
| Termo | Descrição |
|---|---|
| xi | ia observação |
| N | número de observações não ausentes |
Desvio padrão (StDev)
O desvio padrão da amostra fornece uma medida da dispersão dos seus dados. Ela é igual à raiz quadrada da variância da amostra.
Fórmula
 , então, o desvio padrão dos dados da amostra é:
, então, o desvio padrão dos dados da amostra é:
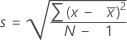
Notação
| Termo | Descrição |
|---|---|
| x i | i a observação |
 | média das observações |
| N | número de observações não ausentes |
Variância
A variância mede o quanto os dados estão dispersos em relação à sua média. A variância é igual ao desvio padrão ao quadrado.
Fórmula
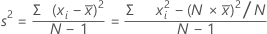
Notação
| Termo | Descrição |
|---|---|
| xi | ia observação |
 | média das observações |
| N | número de observações não ausentes |
Soma
Fórmula

Notação
| Termo | Descrição |
|---|---|
| xi | i a observação |
Mínimo
O menor valor em seu conjunto de dados.
Mediana
A mediana da amostra fica no meio dos dados: pelo menos metade das observações são menores ou iguais a ela, e pelo menos metade são maiores ou iguais a ela.
Suponha que você tenha uma coluna que contém valores de N. Para calcular a mediana, primeiro ordene seus valores de dados do menor ao maior. Se N for ímpar, a mediana da amostra é o valor no meio. Se N for par, a mediana da amostra é a média dos dois valores do meio.
Por exemplo, quando N = 5 e você tem dados x1, x2, x3, x4 e x5, a mediana = x3.
Quando N = 6 e você ordenou os dados x1, x2, x3, x4, x5 e x6:

em que x3 e x4 são a terceira e quarta observações.
Máximo
O maior valor em seu conjunto de dados.
Média
Fórmula
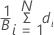
Notação
| Termo | Descrição |
|---|---|
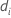 | diferença nas médias das iésimas reamostras |
| B | Número de reamostras |
| N | Número de observações para um grupo da amostra original |
Desvio padrão de uma distribuição Bootstrap
Fórmula

Notação
| Termo | Descrição |
|---|---|
 | média das diferenças das reamostras |
| B | número de reamostras |
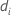 | diferença nas médias da iésima reamostra |
Intervalo de confiança
Fórmula
Ordene a diferença nas médias das reamostras em ordem crescente. d1 é o menor número, dB é o maior número.
Limite inferior: dl onde = 
Limite superior: du onde = 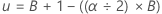
Observação
Para um caso unilateral (somente um limite superior ou um limite inferior), use α no lugar de α/2.
Quando l ou u não são inteiros, o Minitab faz uma interpolação linear entre dois números em cada lado de l ou u. A fórmula é:
dy + z(dy+1 - dy)
Por exemplo, se l = 5,25, o limite inferior é igual a d5 + ,25(d6 - d5).
O Minitab não exibe o intervalo de confiança quando  ou
ou 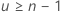 .
.
Notação
| Termo | Descrição |
|---|---|
| α | 1 – nível de confiança/100 |
| B | número de reamostras |
| dy | a i-ésima diferença quando os dados estão ordenados do menor para o maior |
| y | o valor truncado de l ou u |
| z | l-y ou u - y |
