Neste tópico
Histograma
Um histograma divide os valores amostrais em diversos intervalos e representa a frequência dos valores de dados em cada intervalo com uma barra.
Interpretação
50 reamostras
1000 reamostras
Normalmente, é mais fácil determinar a distribuição com mais reamostras. Por exemplo, nesses dados, a distribuição é ambígua para 50 amostras. Com 1000 reamostras, a forma parece aproximadamente normal.
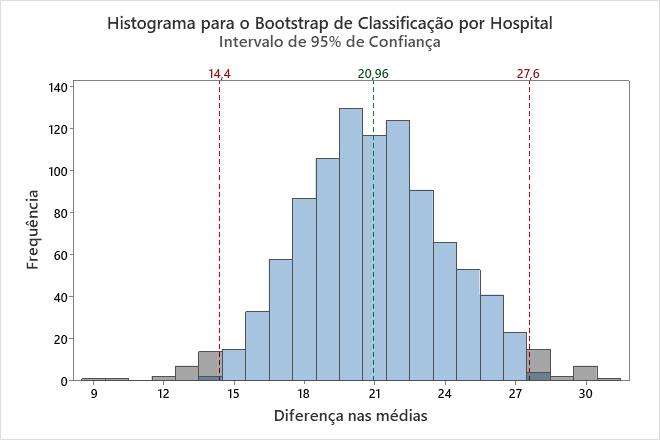
Neste histograma, a distribuição de bootstrap parece ser normal.
Gráfico de valores individuais
Um gráfico de valores individuais exibe os valores individuais na amostra. Cada círculo representa uma observação. Um gráfico de valores individuais é especialmente útil quando você tiver relativamente poucas observações e também precisar avaliar o efeito de cada observação.
Observação
O Minitab mostra um gráfico de valores individuais apenas quando você coleta somente uma reamostra. O Minitab exibe os dados originais e os dados da reamostra.
Interpretação
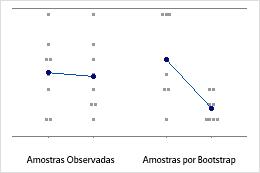
Tamanho amostral 8
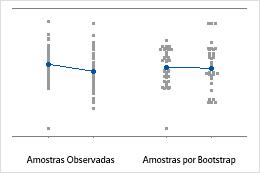
Tamanho amostral 50
Número de Reamostras
O número de reamostras é o número de vezes que o Minitab coleta uma amostra aleatória com a substituição do conjunto de dados original. Normalmente, um grande número de reamostras funciona melhor. O tamanho da amostra para cada reamostra é igual ao tamanho da amostra do conjunto de dados original. O número de reamostras é igual ao número de observações no histograma.
Média
A média é a soma de todas as diferenças nas médias da amostra de bootstrapping, dividida pelo número de reamostras.
Interpretação
O Minitab exibe dois valores diferentes para a diferença em médias, a diferença das amostras observadas e a diferença da distribuição de bootstrap (Média). Ambos valores são uma estimativa da diferença nas médias da população e normalmente serão similares. Se houver uma diferença grande entre estes dois valores, você deve aumentar o tamanho da amostra de sua amostra original.
Como a média está baseada em dados da amostra e não na população total, é improvável que a média seja igual às médias da população. Para estimar melhor a diferença nas médias da população, use o intervalo de confiança.
StDev (amostra por bootstrap)
O desvio padrão é a medida mais comum de dispersão, ou o quanto os dados estão dispersos sobre a média. O símbolo σ (sigma) é frequentemente usado para representar o desvio padrão de uma população, enquanto s é usado para representar o desvio padrão de uma amostra. A variação que é aleatória ou natural de um processo é frequentemente referida como ruído. Como o desvio padrão está nas mesmas unidades que os dados, ele é normalmente mais fácil de interpretar do que a variância.
O desvio padrão das amostras de bootstrap (também conhecido como erro padrão de bootstrap) é uma estimativa do desvio padrão da distribuição amostral da diferença de médias.
Interpretação
Use o desvio padrão para determinar o quão dispersas as diferenças da amostra de bootstrap estão da média global de diferenças. Um valor de desvio padrão mas alto indica maior dispersão nas diferenças. Uma boa regra de ouro de uma distribuição normal é que aproximadamente 68% dos valores estão dentro de um desvio padrão da média global das diferenças, 95% dos valores estão dentro de dois desvios padrão e 99,7% dos valores estão dentro de três desvios padrão.
Use o desvio padrão das amostras de bootstrap para determinar o quão precisamente as diferenças da amostra de bootstrap estimam a diferença de população em médias. Um valor menor indica uma estimativa mais precisa da diferença de população. Normalmente, um desvio padrão maior resulta em um erro padrão de bootstrap maior e uma estimativa menos precisa da diferença de população. Um tamanho amostral maior resulta em um erro padrão de bootstrap menor e em uma estimativa mais precisa da diferença de população.
Intervalo de confiança (IC) e limites
Os intervalos de confiança são baseados na distribuição de amostragem de uma estatística. Se uma estatística não tem viés como um estimador de um parâmetro, sua distribuição de amostragem estará centrada no valor verdadeiro do parâmetro. Uma distribuição de bootstrapping aproxima a distribuição amostral da estatística. Portanto, o meio dos 95% dos valores da distribuição de bootstrapping fornece um intervalo de confiança a 95% para o parâmetro. O intervalo de confiança ajuda a avaliar a significância prática de sua estimativa do parâmetro populacional. Use seu conhecimento especializado para determinar se o intervalo de confiança inclui valores que tenham significância prática para a sua situação.
Observação
O Minitab não calcula o intervalo de confiança quando o número de reamostras é muito pequeno para obter um intervalo de confiança preciso.
Amostras observadas
| Hospital | N | Média | DesvPad | Variância | Mínimo | Mediana | Máximo |
|---|---|---|---|---|---|---|---|
| A | 20 | 80,30 | 8,18 | 66,96 | 62,00 | 79,00 | 98,00 |
| B | 20 | 59,30 | 12,43 | 154,54 | 35,00 | 58,50 | 89,00 |
Diferença nas médias observadas
| Média de A - Média de B = 21 |
|---|
Amostras por Bootstrap para Diferença entre Médias
| Número de reamostras | Média | DesvPad | IC de 95% para a Diferença |
|---|---|---|---|
| 1000 | 20,960 | 3,279 | (14,400; 27,600) |
Nesses resultados, a estimativa da diferença da população é 20,96. Você pode ter 95% de confiança que a diferença da população está entre 14,4 e 27,6.
