Neste tópico
Etapa 1: examinar a forma da sua distribuição bootstrap
50 reamostras
1000 reamostras
É mais fácil determinar a distribuição com mais reamostras. Por exemplo, nestes dados, a distribuição é ambígua para 50 reamostras. Com 1000 reamostras, o formato parece aproximadamente normal.
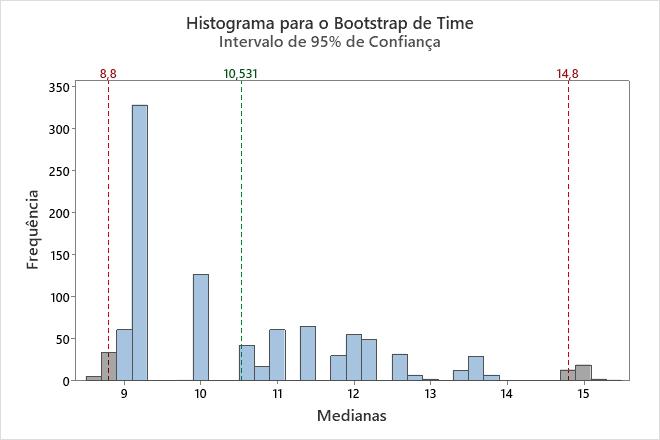
Neste histograma, a distribuição de bootstrap não parece ser normal. A amostra original tem somente 16 pontos de dados. Para obter um intervalo de confiança, é necessário coletar uma amostra maior e realizar a análise novamente.
Etapa 2: Determinar o intervalo de confiança para o parâmetro da população
Primeiro, considere a estatística da amostra de bootstrap e depois examine o intervalo de confiança.
A estatística da amostra de bootstrap é uma estimativa do parâmetro da população. Como a estatística está baseada em dados da amostra e não da população total, é improvável que a estatística da amostra seja igual ao parâmetro da população. Para estimar melhor o parâmetro da população, use o intervalo de confiança.
Os intervalos de confiança são baseados na distribuição de amostragem de uma estatística. Se uma estatística não tem vício como um estimador de um parâmetro, sua distribuição de amostragem estará centrada no valor verdadeiro do parâmetro. Uma distribuição bootstrap aproxima a distribuição amostral da estatística. Portanto, o meio dos 95% dos valores da distribuição bootstrap fornece um intervalo de confiança a 95% para o parâmetro. O intervalo de confiança ajuda a avaliar a significância prática de sua estimativa do parâmetro populacional. Use seu conhecimento especializado para determinar se o intervalo de confiança inclui valores que tenham significância prática para a sua situação.
Observação
O Minitab não calcula o intervalo de confiança quando o número de reamostras é muito pequeno para obter um intervalo de confiança preciso.
Amostra observada
| Variável | N | Média | DesvPad | Variância | Soma | Mínimo | Mediana | Máximo |
|---|---|---|---|---|---|---|---|---|
| Time | 16 | 11,331 | 3,115 | 9,702 | 181,300 | 7,700 | 10,050 | 16,000 |
Amostras por bootstrap da média
| Número de reamostras | Média | DesvPad | IC de 95% para μ |
|---|---|---|---|
| 1000 | 11,3095 | 0,7625 | (9,8562; 12,8562) |
Principais resultados: Média, Intervalo de confiança a 95%
Nestes resultados, a estimativa para a média populacional é aproximadamente 11,3. Você pode ter 95% de confiança que a média da população está entre aproximadamente 9,9 e 12,9.
