Neste tópico
Etapa 1: Procure por outliers e deslocamentos súbitos
Use o conhecimento do processo para determinar se observações ou deslocamentos incomuns indicam erros ou uma mudança real no processo.
Outliers
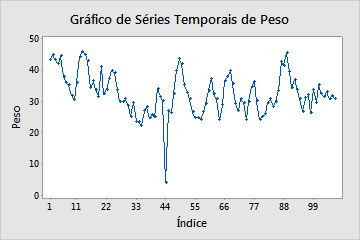
Procure por observações incomuns, também chamadas de outliers. Os outliers podem exercer um efeito desproporcional sobre modelos de séries temporais e produzir resultados enganosos. Tente identificar a causa de todos os outliers e corrigir eventuais erros de entrada de dados ou erros de medição. Considere a remoção de valores de dados que estejam associados a eventos anormais que ocorrem somente uma vez, também chamados de causas especiais.
Deslocamentos súbitos
Procure por deslocamentos súbitos na série ou mudanças bruscas de tendências. Tente identificar a causa de tais mudanças.
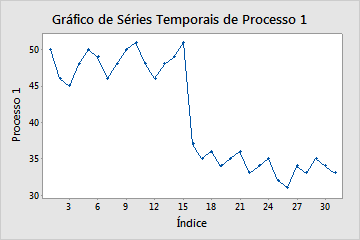
Por exemplo, o gráfico de série de temporal a seguir mostra uma mudança drástica no custo do processo, após 15 meses. Você deve investigar a razão para isso.
Passo 2: Procure por tendências
A tendência é um aumento ou a diminuição a longo prazo dos valores de dados. Uma tendência pode ser linear ou pode apresentar alguma curvatura. Se seus dados apresentarem uma tendência, é possível usar uma análise de séries temporais para modelar os dados e gerar previsões. Para obter mais informações sobre quais análises devem ser usadas, acesse Quais análises de séries temporais devo usar?.
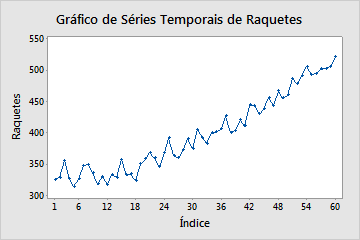
O gráfico de séries temporais a seguir mostra uma clara tendência ascendente. Também pode haver uma leve curva nos dados, porque o aumento nos valores de dados parece acelerar ao longo do tempo. Se houver curvatura, um modelo quadrático é o mais apropriado.
Passo 3: Procure por padrões sazonais ou movimentos cíclicos
Um padrão sazonal é uma ascensão e queda nos valores de dados que se repete regularmente durante o mesmo período de tempo. Por exemplo, os pedidos em uma loja de autopeças são baixos todas as segundas-feiras, aumentam durante a semana e chegam ao pico às sextas-feiras. Os padrões sazonais sempre têm um período fixo e conhecido. Em contraste, os movimentos cíclicos são ciclos de ascensão e queda de valores de dados que não se repetem em intervalos regulares. Normalmente, os movimentos cíclicos são mais longos e mais variáveis do que os padrões sazonais.
Você pode usar uma análise de séries temporais para modelar padrões e gerar previsões. Para obter mais informações sobre quais análises devem ser usadas, acesse Quais análises de séries temporais devo usar?.
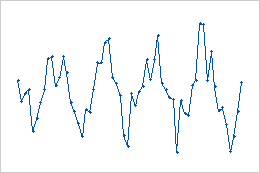
- Padrão sazonal
- Estes dados mostram um padrão sazonal. O padrão se repete a cada 12 meses.
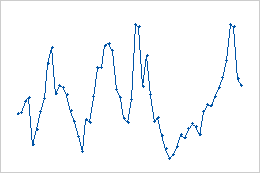
- Movimentos cíclicos
- Estes dados mostram movimentos cíclicos. Os ciclos não se repetem em intervalos regulares e não têm a mesma forma.
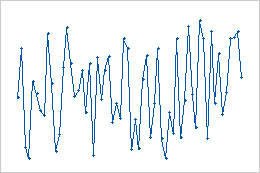
- Variação aleatória
- Estes dados mostram a variação aleatória. Não há padrões ou ciclos.
Passo 4: Avalie se as mudanças sazonais são aditivas ou multiplicativas
Se a magnitude das mudanças sazonais for constante, as mudanças sazonais são aditivas. Se a magnitude das mudanças sazonais for maior quando os valores de dados forem maiores, então, as mudanças sazonais são multiplicativas. A variabilidade extra pode tornar as mudanças sazonais multiplicativas mais difíceis de serem previstas com precisão.
Se o padrão nos dados não for muito óbvio e for difícil escolher entre procedimentos aditivos e multiplicativos para modelar seus dados, é possível tentar os dois e optar por aquele que apresentar menores medidas de precisão. Para obter mais informações, acesse Quais análises de séries temporais devo usar?.
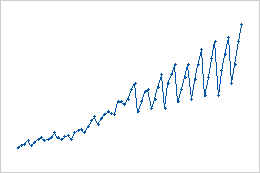
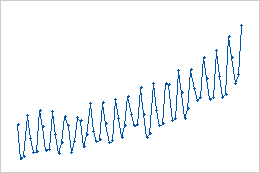
- Mudanças aditivas
- Neste exemplo de mudanças sazonais aditivas, os valores de dados tendem a aumentar com o tempo, mas a magnitude da mudança sazonal permanece a mesma.
- Mudanças multiplicativas
- Neste exemplo de mudanças sazonais multiplicativas, a magnitude da mudança sazonal aumenta com o tempo à medida que os valores de dados aumentam.