Um gráfico de probabilidade cria uma função distribuição acumulada (FDA) estimada a partir da sua amostra representando graficamente o valor de cada observação (incluindo valores repetidos) contra sua probabilidade acumulada estimada.
O Minitab calcula a probabilidade acumulada estimada usando uma das fórmulas a seguir, de acordo com o que é selecionado em (o padrão é o posto da mediana). Para cada fórmula, seja n igual ao número de observações e i igual à ordem de classificação de cada observação de tal forma que i = 1 para o menor valor e i = n para a maior.
- Posto da mediana (Benard)
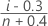
- Posto da média (Herd-Johnson)

- Kaplan-Meier modificado (Hazen)
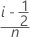
- Kaplan-Meier

Observação
Os resultados do método de Kaplan-Meier em p = 1 para a maior observação. Uma vez que o valor resultante não pode ser usado no gráfico, o Minitab, em vez disso, calcula o maior p como 90% da distância entre o p anterior e 1.
A linha de distribuição ajustada representa o FDA para a distribuição teórica selecionada com os parâmetros indicados (estimados ou históricos). Se não forem fornecidos os parâmetros históricos, o Minitab calcula os parâmetros usando a estimativa de mínimos quadrados (distribuição normal ou lognormal) ou a estimativa da máxima verossimilhança (outras distribuições).
Os valores de y (e em alguns casos os valores de x) são transformados de modo que a linha ajustada seja linear. Os rótulos de marcadores de eixos, no entanto, permanecem consistentes com os valores não transformados. Assim, na medida em que a distribuição selecionada ajusta seus dados, os pontos representados graficamente formam uma linha reta.
A tabela a seguir mostra as transformações utilizadas para cada distribuição.
| Distribuição | Coordenada x | Coordenada y (pontuação) |
|---|---|---|
| Normal | dados | |
| Lognormal | ln(dados) | |
| Lognormal para 3 parâmetros | ln(dados - limite) | |
| Gama | ln(dados) | G-1(p), k |
| Gama para 3 parâmetros | ln(dados - limite) | G-1(p), k |
| Exponencial | ln(dados) | ln(-ln(1 - p)) |
| Exponencial com 2 parâmetros | ln(dados - limite) | ln(-ln(1 - p)) |
| Menor valor extremo | dados | ln(-ln(1 - p)) |
| Weibull | ln(dados) | ln(-ln(1 - p)) |
| Weibull com 3 parâmetros | ln(dados - limite) | ln(-ln(1 - p)) |
| Maior valor extremo | dados | -ln(-ln(p)) |
| Logística | dados |
 |
| Loglogística | ln(dados) |
 |
| Loglogística para 3 parâmetros | ln(dados - limite) |
 |
Importante
Se você representar graficamente dados não ajustados para o limite, o ajuste da distribuição não é indicado por uma linha reta.
Notação
| Termo | Descrição |
|---|---|
| dados | valor de dados para a observação |
| In(x) | log natural de x |
| valor retornado para p pela FDA inversa para a distribuição normal padrão. | |
| G-1(p),k | valor retornado para p pela FDA inversa para uma distribuição Gama com forma = k e escala = 1. O Minitab utiliza o parâmetro de forma estimado, a menos que você insira um valor histórico. |
