Neste tópico
Etapa 2: Determine se seus dados não seguem a distribuição
- Valor-p ≤ α: os dados não seguem a distribuição (você deve rejeitar H0)
- Se o valor-p for menor ou igual ao nível de significância, você deve rejeitar a hipótese nula e concluir que os seus dados não seguem a distribuição.
- Valor-p > α: não é possível concluir que os dados não seguem a distribuição (você não deve rejeitar H0)
- Se o valor-p for maior do que o nível de significância, você não deve rejeitar a hipótese nula porque não há evidências suficientes para concluir que os seus dados não seguem a distribuição. Entretanto, não é possível concluir que os dados não seguem a distribuição.
Para obter mais informações sobre como especificar diferentes distribuições e parâmetros para o teste, acesse Linhas de distribuição ajustadas.
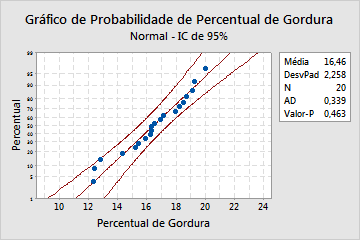
Principais resultados: valor-p
Nestes resultados, a hipótese nula afirma que os dados seguem uma distribuição de normal. Como o valor-p é 0,463, que é maior do que o nível de significância de 0,05, a decisão é deixar de rejeitar a hipótese nula. Não é possível concluir que os dados não seguem uma distribuição normal.
Cautela
O tamanho amostral afeta o poder do teste. Amostras extremamente pequenas podem ter poder inadequado para detectar desvios significativos da distribuição. Amostras extremamente grandes podem ter poder excessivo para detectar pequenos desvios inconsequentes da distribuição. Por conseguinte, utilize os resultados visuais no gráfico de probabilidade, bem como os valores-p para avaliar o ajuste de distribuição, como mostrado na Etapa 2.
Etapa 2: Visualize o ajuste da distribuição normal
Examine o gráfico de probabilidade e avalie o quão próximo os pontos de dados seguem a linha de distribuição ajustada. Se a distribuição teórica especificada é um bom ajuste, os pontos de cair próximos ao longo da linha reta. Por exemplo, os pontos no gráfico de probabilidade normal a seguir seguem bem a linha ajustada. A distribuição normal parece ser um bom ajuste para os dados.
Observação
A linha de distribuição ajustada é a linha reta do meio no meio do gráfico. As linhas contínuas externas no gráfico são intervalos de confiança para os percentis individuais, não para a distribuição como um todo, e não devem ser utilizadas para avaliar o ajuste da distribuição.
Para obter mais informações sobre a avaliação visual dos valores no gráfico de probabilidade, acesseGráficos de probabilidade normal e o "teste do lápis gordo".
Etapa 3: Exiba os percentis estimados para a população
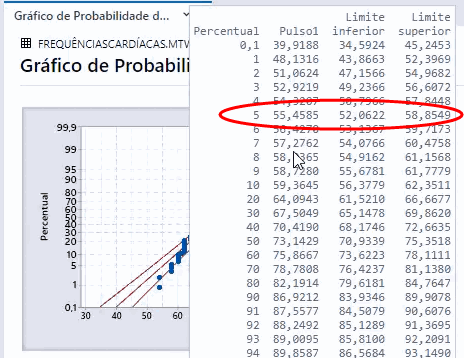
No Minitab, mantenha o cursor sobre a linha de distribuição ajustada para ver uma tabela de percentis e valores.
Por exemplo, o gráfico de probabilidade a seguir mostra as frequências cardíacas dos sujeitos de teste durante a caminhada em uma esteira. Para uma distribuição normal com uma média e desvio padrão igual a os dados, a expectativa era de que 5% da população apresentasse uma frequência cardíaca de 54,76 ou menos.
Observação
Os percentis estimados da população são precisos somente se os dados seguirem de perto a distribuição.
