Etapa 1: Avalie as características chaves
Examine o centro da distribuição. Avalie como o tamanho amostral pode afetar a aparência do gráfico de intervalos.
Centro
- Intervalo de confiança
- O intervalo de confiança é uma faixa de valores que tende a incluir a média da população.
- Média da amostra
- A média da amostra é representada por um símbolo.
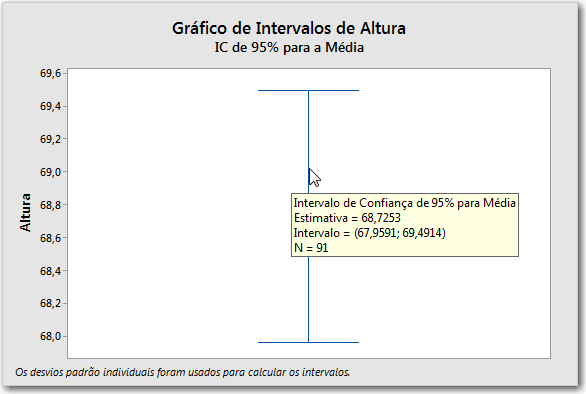
Investigue os intervalos de confiança que são surpreendentes ou inesperados. Por exemplo, se um intervalo de confiança para a média de uma amostra de tempo de espera do cliente for substancialmente diferente dos intervalos de confiança das amostras anteriores, você deve tentar determinar a causa da diferença.
Tamanho de amostra (n)
O tamanho de amostra pode afetar a aparência do gráfico.
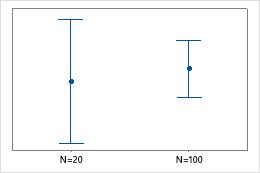
Geralmente, quanto maior o tamanho amostral, menor e mais preciso é o intervalo de confiança. Se o intervalo de confiança for muito amplo, tente coletar uma amostra maior. Grandes diferenças nos tamanhos amostrais entre os grupos (ou múltiplas variáveis Y) podem afetar as larguras dos intervalos, e produzir resultados enganosos. Se os tamanhos das amostras para os grupos (ou múltiplas variáveis Y) forem aproximadamente iguais, é possível ter mais certeza de que diferenças nas larguras dos intervalos sejam principalmente devidas às diferenças na variação.
Passo 2: Avaliar e comparar grupos
Se seu gráfico de intervalos tiver grupos, avalie e compare o centro e dispersão dos grupos.
Centros
Determine se os intervalos de confiança se sobrepõem. Se os intervalos de duas médias não se sobrepõem, as médias da população podem ser estatisticamente significativas.
Por exemplo, no primeiro gráfico de intervalos, o primeiro e segundo intervalos sobrepõem-se entre si, mas que não se sobrepõem com o terceiro intervalo. Por conseguinte, a média do terceiro grupo pode ser significativamente diferente do que as médias dos outros dois grupos. No segundo gráfico de intervalos, os intervalos não se sobrepõem. Por conseguinte, as diferenças nas médias podem ser estatisticamente significativas.
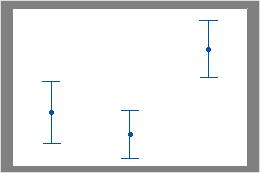
Alguns intervalos se sobrepõem
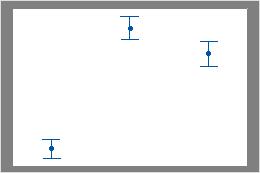
Nenhum intervalo se sobrepõe
- Use um teste t de 2 amostras se você tiver apenas dois grupos.
- Use um ANOVA com um fator se você tiver três ou mais grupos.
Dispersões
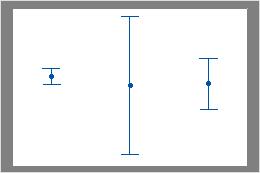
Procure por diferenças entre as dispersões dos grupos.
Os intervalos neste gráfico têm centros semelhantes, mas dispersões diferentes.
Dica
Para determinar se uma diferença na largura do intervalo é causada por uma diferença na variação da amostra ou por uma diferença no tamanho amostral, clique duas vezes em um intervalo. Na guia Opções, clique em Erro de combinação nos grupos. Isto recria os intervalos utilizando o desvio padrão combinado em vez dos desvios padrão individuais. Todas as diferenças nas larguras observadas agora são estritamente devidas a diferentes tamanhos amostrais.
- Use um teste para 2 variâncias se você tiver apenas dois grupos.
- Use um teste de igualdade de variâncias caso tenha três ou mais grupos.
