Distribuição exponencial
Utilize a distribuição exponencial para modelar o tempo entre os eventos em um processo de Poisson contínuo. Supõe-se que ocorram eventos independentes a uma taxa constante.
Esta distribuição tem uma grande variedade de aplicações, incluindo a análise de confiabilidade de produtos e sistemas, teoria das filas e cadeias de Markov.
- Quanto tempo leva para componentes eletrônicos falharem
- O intervalo de tempo entre as chegadas dos clientes a um terminal
- Tempo de serviço para os clientes esperando na fila
- O tempo até padrão em um pagamento (modelagem de risco de crédito)
- Tempo até a decadência de um núcleo radioativo
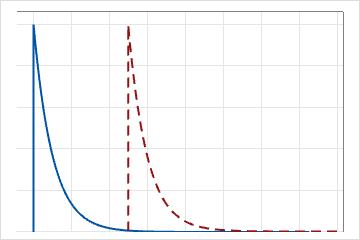
Para a distribuição exponencial de 1 parâmetro, o limite é zero e a distribuição é definido pelo seu parâmetro de escala. Para a distribuição exponencial de 1 parâmetro, o parâmetro de escala é igual à média.
O que significa memoryless?
Uma importante propriedade da distribuição exponencial é que ela é memoryless. A chance de um evento não depende de ensaios passados. Portanto, a taxa de ocorrência permanece constante.
A propriedade memoryless indica que a vida útil restante de um componente é independente da sua idade atual. Por exemplo, os ensaios aleatórios de jogar uma moeda demonstram a propriedade memoryless. Um sistema que sofre desgaste e, portanto, torna-se mais propenso a falhar posteriormente em sua vida útil, não é memoryless.
Distribuição gama
Use a distribuição gama para modelar valores de dados positivos que são assimétricos à direita e maiores que 0. A distribuição gama é comumente usada em estudos de sobrevivência de confiabilidade. Por exemplo, a distribuição gama pode descrever o tempo de um componente elétrico de falhar. A maioria dos componentes elétricos de um determinado tipo falharão na mesma época, mas alguns vão demorar muito tempo para falhar.
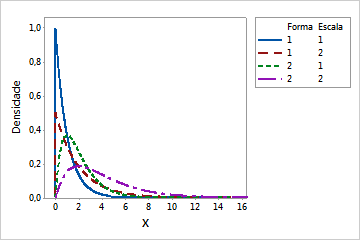
Quando o parâmetro de forma é um número inteiro positivo, a distribuição gama é, algumas vezes, chamada de distribuição Erlang. A distribuição Erlang é usada normalmente em aplicações da teoria de filas.
Distribuição logística
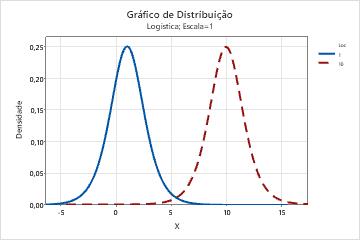
Use a distribuição logística para modelar distribuições de dados que tenham caudas mais longas e maior curtose do que a distribuição normal.
- Efeito do parâmetro escala
- Este gráfico a seguir mostra o efeito de diferentes valores do parâmetro de escala na distribuição logística.
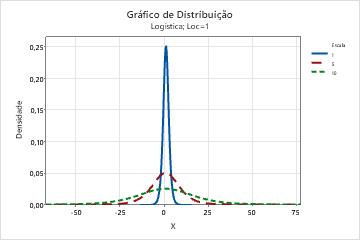
- Efeito do parâmetro localização
- Este gráfico a seguir mostra o efeito de diferentes valores do parâmetro de localização sobre a distribuição logística.
Distribuição loglogística
Use a distribuição loglogística quando o logaritmo da variável for logisticamente distribuído. Por exemplo, a distribuição loglogística é utilizada em modelos de crescimento e para modelar respostas binárias em domínios como a bioestatística e economia.
A distribuição loglogística é uma distribuição contínua, definida por seus parâmetros de escala e localização. A distribuição loglogística de 3 parâmetros é definida por seus parâmetros de escala, localização e limite.
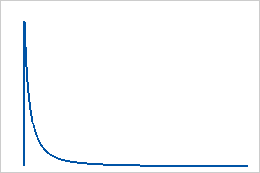
A distribuição loglogística é também conhecida como a distribuição de Fisk.
Distribuição lognormal
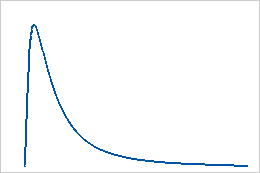
Utilize a distribuição lognormal se o logaritmo da variável aleatória for normalmente distribuído. Use quando as variáveis aleatórias forem maiores do que 0. Por exemplo, a distribuição lognormal é usada para análise de confiabilidade e em aplicações financeiras, como a modelagem do comportamento de estoque.
A distribuição lognormal é uma distribuição contínua, definida por seus parâmetros de escala e localização. A distribuição lognormal de 3 parâmetros é definida por seus parâmetros de localização, escala e limite.
Distribuição normal
A distribuição normal é uma distribuição contínua, que é especificada pela média (μ) e o desvio padrão (σ). A média é o pico ou centro da curva em forma de sino. O desvio padrão determina a dispersão da distribuição.
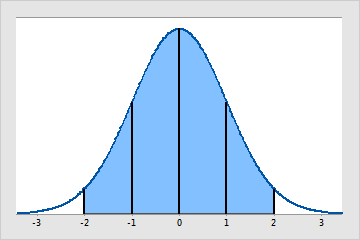
A distribuição normal é a distribuição estatística mais comum porque a normalidade aproximada ocorre naturalmente em muitas situações de medição física, biológica e social. Muitas análises estatísticas assumem que os dados são provenientes de populações com distribuição aproximadamente normal.
Distribuições do menor e maior valores extremos
A distribuição de maior valor extremos e a distribuição de menor valor extremo estão intimamente relacionadas. Por exemplo, se X tiver a distribuição de maior de valor extremo, X tem uma distribuição de menor valor extremo e vice-versa.
Distribuição do menor valor extremo
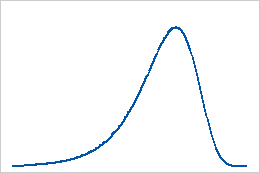
Distribuição do maior valor extremo
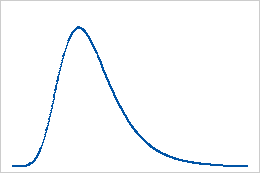
Distribuição Weibull
A distribuição Weibull é uma distribuição versátil que pode ser usada para modelar uma ampla variedade de aplicativos em engenharia, pesquisa médica, controle de qualidade, finanças e climatologia. Por exemplo, a distribuição é normalmente utilizada com análises de confiabilidade para modelar dados de tempo até a falha. A distribuição Weibull também é usada para modelar dados de processo assimétricos na análise de capacidade.
A distribuição Weibull é descrita pelos parâmetros de forma, escala e limite, e também é conhecida como a distribuição Weibull de 3 parâmetros. O caso quando o parâmetro de limite é zero é chamado de distribuição Weibull de 2 parâmetros. A distribuição Weibull de 2 parâmetros é definida apenas para variáveis positivas. Uma distribuição Weibull de 3 parâmetros pode trabalhar com zeros e dados negativos, mas todos os dados para uma distribuição de Weibull de 2 parâmetros devem ser maiores do que zero.
Dependendo dos valores de seus parâmetros, a distribuição Weibull pode assumir diversas formas.
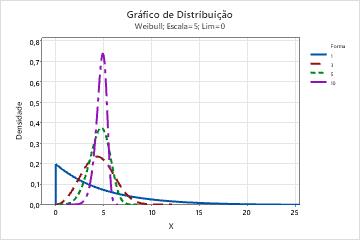
- Efeito do parâmetro de forma
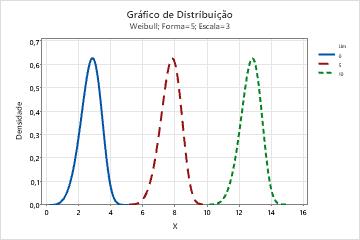
- O parâmetro de forma descreve como seus dados são distribuídos. Uma forma de 3 se aproxima de uma curva normal. Um valor baixo para forma, digamos 1, dá uma curva com assimetria à direita. Um valor alto para forma, digamos 10, dá uma curva com assimetria à esquerda.
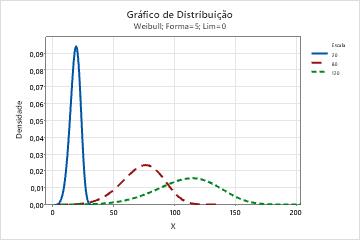
- Efeito do parâmetro escala
- A escala, ou vida característica, é o percentil 63,2 dos dados. A escala define a posição da curva Weibull relativa ao limite, que é análogo à maneira em que a média define a posição de uma curva normal. Uma escala de 20, por exemplo, indica que 63,2% dos equipamentos irá falhar nas primeiras 20 horas após o tempo limite.
- Efeito do parâmetro limite
- O parâmetro de limite descreve o deslocamento da distribuição em relação ao 0. Um limite negativo desloca a distribuição para a esquerda, e um limite positivo desloca a distribuição para a direita. Todos os dados devem ser maiores do que o limite. A distribuição Weibull de 2 parâmetros é a mesma que a Weibull de 3 parâmetros com um limite de 0. Por exemplo, uma distribuição Weibull de 3 parâmetros (3, 100, 50) tem a mesma forma e dispersão que a distribuição Weibull de 2 parâmetros (3, 100), mas é deslocada 50 unidades para a direita.