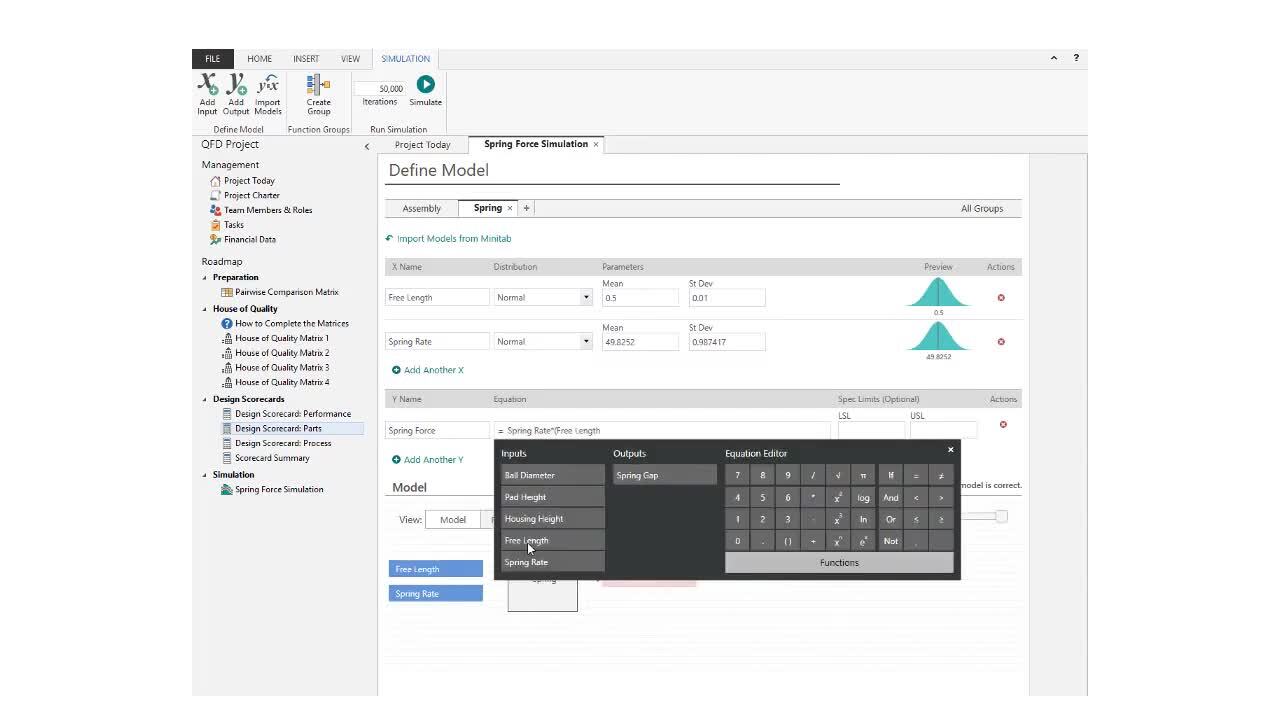
Definir o modelo
Para executar uma simulação, você deve saber a distribuição e parâmetros para cada entrada (X) e as equações que descrevem seu processo.
Escolher uma distribuição
- Se os dados históricos estão disponíveis e representam o desempenho futuro esperado, você pode usar o recurso Usar dados para decidir. Engage automaticamente encontra a distribuição com o melhor ajuste.
- Se os dados históricos não estão disponíveis, procure especialistas em sua organização ou consulte a literatura. Certifique-se de procurar exemplos específicos do setor que correspondam ao seu aplicativo.
Identificar as equações
As equações podem vir do conhecimento do processo ou ser baseadas em um modelo que você criou a partir de um experimento projetado (DOE) ou análise de regressão no Minitab.
Modelos de importação de Minitab
| Modelo | Exceções |
|---|---|
| Fatorial |
|
| Superfície de Resposta |
|
| Regressão |
|
- Variáveis X (entradas), que podem incluir fatores contínuos, fatores categóricos e covariáveis
- Variáveis Y (saídas)
- A equação Y, juntamente com os coeficientes das entradas em unidades não codificadas e o termo constante
Se um modelo contém fatores categóricos, você pode selecionar os níveis de fator para incluir na equação.
Observação
Para comparar os resultados da simulação para a mesma variável Y usando diferentes níveis de fator, selecione a variável Y e o nível de fator para incluir na equação e, em seguida, importe-os. Repita este processo até que você tenha selecionado todos os níveis de fator para comparar.
Executar a simulação
Depois de definir o modelo, você está pronto para executar uma simulação.
- A partir do painel do navegador, selecione Adicionar ferramenta e, em seguida, selecione .
- Selecione Importar modelos de Minitab se deseja usar um modelo do Minitab. Você pode escolher um projeto do Minitab que você adicionou como um documento relacionado ou um que você salvou em seu computador ou uma rede. Para mais informações, acesse “Importar modelos do Minitab”, neste tópico.
- Insira um nome para cada entrada. Se você importou um modelo do Minitab, você pode alterar o nome da entrada importada.
- Escolha uma distribuição para cada entrada e insira os parâmetros. Se você não tem certeza de qual distribuição escolher e tem dados históricos do sistema, selecione Usar dados para decidir. Em seguida, navegue até o arquivo CSV que contém dados. Certifique-se de que os dados representam desempenho futuro esperado. Engage automaticamente encontra a distribuição com o melhor ajuste. Para obter mais informações, acesse “Escolha uma distribuição” neste tópico.
- Insira um nome para cada saída. Se você importou um modelo do Minitab, você pode alterar o nome da variável de saída importada.
- Digite a equação. Use o Editor de equação se necessário. Para obter mais informações, vá para Use o Editor de equação em simulações.
- Insira um limite inferior de especificação, um limite superior de especificação ou ambos. Para obter métricas de desempenho do processo, você deve inserir pelo menos um limite de especificação. Para mais informações, vá para cálculos em simulações “Cpk e Ppk”, neste tópico.
- Use o diagrama para verificar seu modelo.
- No menu Simulação, insira o número de iterações. O número de iterações deve cobrir adequadamente a gama de possíveis valores de entrada e saída e fornecer resultados precisos. O número máximo é de 1.000.000. No entanto, o padrão de 50.000 é suficiente para a maioria dos modelos.
- Selecione .
Criar grupos
Quando você tem uma simulação complexa ou grande, você pode criar grupos para definir o modelo por função. Por exemplo, você pode querer descrever diferentes ações ou comportamento de várias partes dentro da simulação. Com os grupos, você pode categorizar entradas e saídas para ajudá-lo a gerenciar e organizar sua simulação.
- Depois de adicionar uma simulação, escolha . Uma nova guia aparece acima das variáveis X.
- Para renomear esse grupo, clique duas vezes na guia e digite um nome.
-
Para adicionar outro grupo, selecione o ícone de sinal mais
ao lado do novo
grupo.
Se você acidentalmente fechar um grupo, pressione Ctrl+z para desfazer a ação.
- Insira novas entradas e saídas para cada grupo. Se uma entrada ou uma saída for usada em mais de um grupo, você só precisa inseri-la uma vez.
- Digite a equação de saída para cada grupo. Entradas e saídas de todos os grupos estão disponíveis no Editor de equação.
- Use o diagrama para verificar o modelo, por modelo ou função, para cada grupo ou para todos os grupos.Para visualizar todos os grupos, selecione Todos os grupos acima das visualizações de distribuição.O exemplo a seguir mostra todos os grupos por modelo.
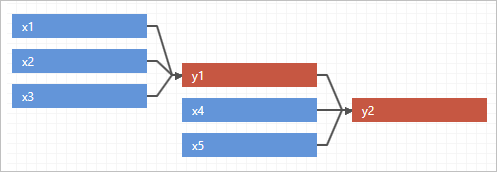O exemplo a seguir mostra todos os grupos por função.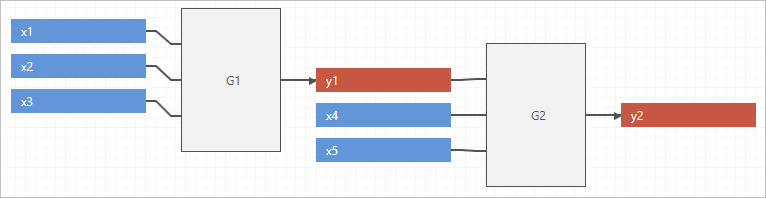
Cpk e cálculos Ppk em simulações
Muitas vezes, nas simulações de Monte Carlo, as respostas simuladas violam a suposição de normalidade. Portanto, Engage utiliza um método não paramétrico para calcular a capacidade na ferramenta de simulação. O método não paramétrico calcula a disseminação da distribuição de saída utilizando os percentis observados 0,135 e 99,865 percentis dos dados simulados, o que é análogo a +/-3 sigma em uma distribuição normal.
Como não há subgrupos e nenhum conceito de variação de longo prazo e de curto prazo no contexto de simulação, os valores Cpk e Ppk são equivalentes na simulação de Monte Carlo Engage. Escolha e, em seguida, selecione o rótulo que você preferir.
Com base na disseminação nos dados e nos limites de especificação definidos no modelo, Engage calcula PPL e PPU para encontrar o Ppk correspondente.
- PPL=(Mediana-LSL)/(Mediana–0,135o Percentil)
- PPU=(USL-Mediana)/(99,865o Percentil-Mediana)
Examinar os resultados
Engage exibe os resultados da simulação, como seus resultados se comparam aos valores geralmente aceitos e orientações para os próximos passos.
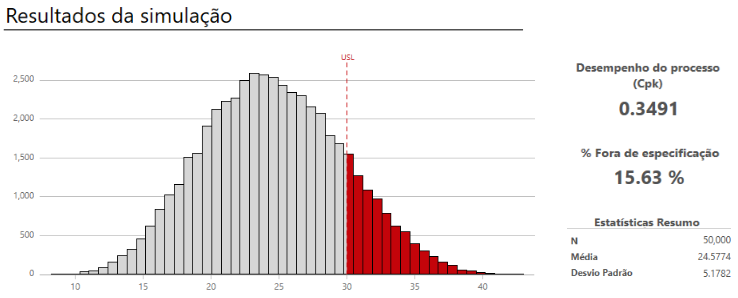
- Veja os resultados no espaço de trabalho. Você pode alternar entre a visão do modelo e a visão de resultados da simulação.
Observação
Cada vez que você repetir a simulação, os resultados variam porque a simulação é baseada em valores selecionados aleatoriamente para as entradas.
- Avalie os resultados e execute qualquer uma das tarefas a seguir.
- Para visualizar DPMO (defeitos por milhão de oportunidades), desempenho observado, estatísticas sumárias, percentis e premissas de modelo, selecione Mais resultados.
- Para ver informações sobre os próximos
passos, segure o ponteiro
. - Para adicionar ou alterar os limites de especificação, escolha . O gráfico e os resultados são atualizados usando os novos limites.
- Para copiar os resultados para que você possa colá-los em apresentações do Microsoft® PowerPoint, clique com o botão direito do mouse no espaço de trabalho e, em seguida, escolha Copiar.
- Para avaliar a estabilidade das estimativas, reexame da simulação com diferentes números de iterações.
- Considere simulações adicionais.
- Identifique as configurações ideais para as entradas que você pode controlar. Para obter mais informações, acesse Realizar otimização de parâmetros.
- Demonstre como as alterações na variabilidade das entradas afetam a variabilidade das saídas. Para obter mais informações, acesse Realizar análise de sensibilidade.
Editar o modelo
Depois de analisar os resultados, você pode querer retornar ao modelo e alterar entradas ou saídas, em seguida, reprisá-lo. Isso permite testar vários cenários possíveis para que você possa obter uma visão sobre o comportamento do seu sistema e tomar melhores decisões.
- Escolha uma das seguintes opções.
- Para mudar o modelo, escolha . Por padrão, Engage sobrescreve os valores existentes no modelo atual.
- Para preservar as configurações atuais e trabalhar em uma cópia, escolha .
- Selecione .
Assista a um vídeo
Assista a um vídeo para saber mais sobre simulações de Monte Carlo.
