매크로 다운로드
Minitab에서 다운로드한 매크로의 위치를 지정해야 합니다. 을 선택합니다. 매크로 위치에서 매크로 파일 저장 위치로 이동합니다.
중요
기존 웹 브라우저를 사용하는 경우 다운로드 단추를 클릭하면 Minitab 매크로와 .mac 파일 확장자를 공유하는 Quicktime에서 해당 파일을 열 수 있습니다. 매크로를 저장하려면 다운로드 단추를 마우스 오른쪽 단추로 클릭하고 다른 이름으로 대상 저장을 선택합니다.
필수 입력
시계열 데이터의 열 하나가 필요합니다.
선택적 입력
- AR K…K
- 추정된 자기 회귀 모수가 있고 분광 모형 확인을 실행하려면 이 모수를 입력합니다.
- DIF K
- 차이 성분이 있는 경우 차이 순서를 입력합니다.
- MA K…K
- 추정된 이동 평균[MA] 모수가 있고 분광 모형 확인을 실행하려면 이 모수를 입력합니다.
- VARIANCE K
- 추정된 분산(기본값 = 1.0)을 입력합니다.
- SMOOTH K
- 이동 평균[MA]의 길이(기본값 = 3)를 입력합니다. 이동 평균[MA]의 길이는 홀수여야 합니다.
- ONEDOC
- 한 페이지에 모든 그래프를 표시하려면 입력합니다.
- SPERIOD C C
- 주기도의 좌표를 저장하려면 입력합니다. 첫 번째 열에는 I(오메가)가 있고 두 번째 열에는 오메가가 있습니다.
- SCUMUL C C C C
- 누적 주기도의 좌표를 저장하려면 입력합니다. 첫 번째 열에는 U(j), 두 번째 열에는 유의 상한, 세 번째 열에는 유의 하한, 네 번째 열에는 X축이 있습니다.
- SSPEC C C C C
- 분광 추정치의 좌표를 저장하려면 입력합니다. 첫 번째 열에는 분광 추정치, 두 번째 열에는 신뢰 상한, 세 번째 열에는 신뢰 하한, 네 번째 열에는 오메가가 있습니다.
- SMODEL C C C C
- 분광 모형 확인의 좌표를 저장하려면 입력합니다. 첫 번째 열에는 F(오메가), 두 번째 열에는 신뢰 상한, 세 번째 열에는 신뢰 하한, 네 번째 열에는 분광 추정치, 다섯 번째 열에는 오메가가 있습니다.
매크로 실행
데이터가 C1에 있다고 가정합니다. 매크로를 실행하려면 을 선택하고 다음을 입력합니다.
%SPECTRAL C1실행을(를) 클릭합니다.
추가 정보
주기도
주기도는 시계열의 순환 성분을 탐지하기 위해 사용할 수 있는 도구입니다. 주기도는 다음과 같이 정의됩니다.
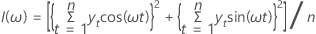
주기도는 ω = 0에 정의되지만, 이 점은 관심의 대상이 아닌 표본 평균에 해당하기 때문에 제외됩니다. n이 홀수인 경우에는 ω =π를 제외합니다.
누적 주기도
누적 주기도는 특정 시계열이 흰색 잡음 수열이라는 가설을 검정하기 위해 주기도를 직접 적용한 것입니다. 누적 주기도는 효과적인 잔차 진단 도구입니다. 누적 주기도는 다음과 같이 정의됩니다.
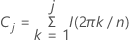
j=1,...,m. 여기서 m은 n/2보다 확실히 작은 최대 정수입니다.
U j의 j /(m −1)에 대한 그림이 누적 주기도로 알려져 있습니다.
또한 흰색 잡음 가설을 검정하기 위한 임계값을 정의할 수 있습니다. 매크로에서 사용하는 유의 수준은 10%(임계값 = 1.224)입니다. 다음과 같은 y-절편의 두 평행선이 임계 영역을 정의합니다.
분광 추정치
분광 추정치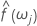 
는 간단히 주기도에 의해 계산되는 세로 좌표의 순서 2p+1(p는 양의 정수임)의 이동 평균[MA]을 취하여 구할 수 있습니다. 이 분광 추정치에 대한 신뢰 한계를 설정할 수도 있습니다.
신뢰 상한 및 하한은 다음과 같이 정의할 수 있습니다.
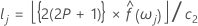
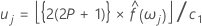
ARMA 공정의 스펙트럼
분광 추정치는 데이터를 기반으로 한 스펙트럼의 추정치입니다. 스펙트럼은 모형 모수에 대한 실제 모집단 값을 기반으로 합니다. AR(p) 공정의 스펙트럼은 다음과 같이 정의할 수 있습니다.
MA(q) 공정의 스펙트럼은 다음과 같이 정의할 수 있습니다.
ARMA (p, q)(p와 q는 순서임) 공정의 스펙트럼은 다음과 같이 정의할 수 있습니다.
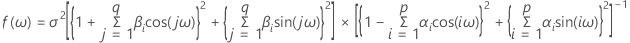
ARIMA 공정에 대한 분광 모형 확인
관측된 시계열에서 계산된 분광 추정치를 모형 모수 기반의 실제 스펙트럼과 비교할 수 있습니다. 직관적으로, 분광 추정치가 실제 스펙트럼과 통계적으로 비슷한 경우 추정된 모형 모수가 시계열을 모형화하는 데 적절하다는 결론을 내릴 수 있습니다.
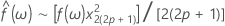
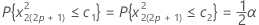
따라서 신뢰 한계를 설정하여 분광 추정치가 이러한 한계 내에 들어가는지 여부를 확인할 수 있습니다.
예 1
주기도, 누적 주기도, 분광 추정치의 예를 보려면 데이터 집합 'Cycle 1, late follicular phase'(Diggle, p. 228)을 고려하십시오. 매크로를 실행하려면 를 선택하고 다음을 입력합니다.
%SPECTRAL C1첫째, 주기도(표시되지 않음)는 우세한 봉우리로 인해 이 시계열에 순환 성분이 없음을 나타냅니다. 때로는 순환 성분이 발생하는 시점을 보다 쉽게 확인할 수 있도록 X 축이 보다 유의한 척도로 변환됩니다. 이러한 이유로, 매크로에는 사용자가 축을 변환할 수 있는 저장 옵션이 있으므로, Minitab의 그래픽 기능을 사용하여 그래프를 생성할 수 있습니다. 둘째, 누적 주기도는 유의 한계(평행한 점선으로 표시됨)를 초과하는 일부 데이터 점으로 인해 이 시계열이 흰색 잡음 수열이 아니라는 것을 나타냅니다. 마지막으로, 분광 추정치(기본 3-점 이동 평균[MA]에 의해 계산됨)는 빨간색 선으로 표시되고 신뢰 한계는 점선으로 표시됩니다. 이 그림은 실제 모집단 스펙트럼의 모양을 일부 보여줍니다. 세 그림 모두 Diggle(p. 52, 55, 106)에서 제공된 그림과 일치합니다.
예 2
완전 ARIMA 분석의 경우 데이터 집합 'Cycle 2, early follicular phase' (Diggle, p. 228)을 고려하십시오. 첫째, 주기도, 누적 주기도 및 분광 추정치를 계산합니다. 또한 'Onedoc' 하위 명령을 사용하여 이 세 그림을 한 페이지에 배치합니다. 를 선택하고 다음을 입력합니다.
%SPECTRAL C2;
ONEDOC.
그래프(표시되지 않음)는 주기도와 분광 추정치가 작은 오메가 값에서 우세한 봉우리로 인해 빈도가 낮은 시계열을 나타내고 누적 주기도에 유의한 점이 표시되기 때문에 이 시계열이 흰색 잡음 수열이 아니라는 것을 분명히 나타냅니다. 따라서, MINITAB에서 ARIMA 알고리즘을 사용하여 이 시계열을 모형화합니다. 다양한 모형을 살펴본 결과 AR(1)이 가장 적합한 모형입니다.
이제 매크로를 사용하여 이 경험적 모형을 평가합니다. 자기 회귀 모수와 분산의 추정치가 (ARIMA 출력에서) 다음 명령어로 어떻게 입력되는지 확인합니다. 를 선택하고 다음을 입력합니다.
%SPECTRAL C2;
AR 0.5860;
VARIANCE 0.20603;
ONEDOC.
그 결과 이미 표시된 그래프가 분광 모형 확인과 함께 다시 표시됩니다. 분광 모형 확인과 관련하여 빨간색 원은 분광 추정치를 나타내고 검은색 실선은 추정된 ARIMA 모형 모수를 기반으로 한 '실제' 스펙트럼을 나타냅니다. 점선은 '실제' 스펙트럼에 대한 신뢰 한계를 나타냅니다. 거의 모든 세 점 이동 평균[MA](빨간색 원)이 실제 스펙트럼에 대한 신뢰 구간 내에 포함되기 때문에 모형이 유효하다는 결론을 내릴 수 있습니다. 마지막으로 잔차에 대해 매크로를 실행하여 흰색 잡음 잔차인지 확인하려고 합니다. 누적 주기도는 사실 잔차가 흰색 잡음 수열을 따른다는 것을 나타냅니다.
참고 문헌
Diggle, P. J. Time Series, A Biostatistical Introduction. Oxford: Clarendon Press, 1990.
