매크로 다운로드
Minitab에서 다운로드한 매크로의 위치를 지정해야 합니다. 을 선택합니다. 매크로 위치에서 매크로 파일 저장 위치로 이동합니다.
중요
기존 웹 브라우저를 사용하는 경우 다운로드 단추를 클릭하면 Minitab 매크로와 .mac 파일 확장자를 공유하는 Quicktime에서 해당 파일을 열 수 있습니다. 매크로를 저장하려면 다운로드 단추를 마우스 오른쪽 단추로 클릭하고 다른 이름으로 대상 저장을 선택합니다.
필수 입력
최대 다섯 개의 설계 행렬이 필요합니다.
선택적 입력
- MODEL 모형 유형
- 실험을 수행할 때 검사할 모형을 지정합니다. 기본값은 "교호작용"입니다. 선형, 2차, 교호작용, 순수 2차 등 여러 모형을 입력할 수 있습니다. 각 모형에는 다음과 같은 항이 포함됩니다.
- 선형: 상수 및 선형 항
- 교호작용: 상수, 선형 및 교차곱 항
- 2차: 교호작용 더하기 제곱 항
- 순수 2차: 상수, 선형 및 제곱 항
- RESOLUTION K
- 고유한 각 반지름 값에서 최대값, 최소값 및 누적 예측 분산을 추정하기 위해 사용되는 표본 설계점의 수를 지정하기 위해 사용합니다. 회전 가능한 설계의 경우 작은 해를 선택할 수 있습니다. 회전 불가능한 설계의 경우 요인 수가 증가함에 따라 해를 증가시켜야 할 수도 있습니다. 기본값은 500개의 설계점입니다.
- INCREMENT K
- 반지름 증분을 지정하기 위해 사용합니다. 해가 더 크거나 더 작은 그래프를 표시하기 위해 이 값을 변경할 수 있습니다. 기본값은 0.1 코드화된 단위입니다.
- MAXDIST K
- 최대 반지름 거리를 나타냅니다. 기본적으로 이 값은 설계의 가장 멀리 떨어져 있는 설계점까지의 최대 거리로 정의됩니다. 여러 설계를 기반으로 하는 VDG의 경우, MAXDIST는 모든 설계로부터의 최대 거리로 설정됩니다.
매크로 실행
CCD 요인이 행렬 M1에 복사되고 Box-Behnken 설계 요인이 M2에 복사되었다고 가정합니다. 매크로를 실행하려면 을 선택하고 다음을 입력합니다.
%VDG M1 M2;
MODEL "2차";
RESOLUTION 150.실행을(를) 클릭합니다.
추가 정보
분산 산포 그래프 및 실험 설계
분산 산포 그래프는 실험계획법을 선택하는 과정에 사용되는 그래픽 도구입니다. 이 그래프는 설계 공간에서 실험계획법의 척도화된 예측 분산을 표시하며, 일반적으로 반응 표면 설계를 비교하기 위해 사용됩니다. 그러나 분산 산포 그래프는 선형 모형, 교호작용 항이 있는 선형 모형, 2차 항이 있는 선형 모형, 완전 2차 모형과 같은 특정 모형에 대한 여러 설계의 성능을 비교하기 위해서도 사용할 수 있습니다.
VDG의 역사 및 배경
VDG는 처음에 Giovannitti-Jensen and Myers (1989) and Myers et al. (1992)에 의해 설계 공간에서 척도화된 예측 분산의 안정성 스냅샷을 표시하기 위해 개발되었습니다.
수학적으로, 척도화된 예측 분산은 아래 방정식을 사용하여 추정할 수 있습니다.
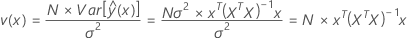
여기서 v(x)는 점 x에서의 척도화된 예측 분산이고, 위에 표시된 대로 반응 데이터에 종속되지 않으며, 설계 행렬 X에만 종속됩니다. 다시 말하면 척도화된 예측 분산은 실험의 런 개수, 공분산 행렬, 예측 분산을 평가하는 점의 함수입니다. VDG에 의해 표시되는 척도 예측 분산은 반응 데이터와 독립적이기 때문에 VDG를 사용하면 설계의 적합도를 미리 평가할 수 있습니다.
일반적으로 VDG는 네 가지 기본 성분으로 구성됩니다.
- · 반지름 r에 대한 구형 분산 그림. 구형 분산은 반지름 r의 구 표면 상의 평균(누적) v(x)입니다.
- · 원점에서 시작하여 여러 r 값에 대한 반지름 r에 대한 최대 예측 분산의 그림(r은 0에서 시작하여 원점에서 가장 멀리 떨어져 있는 설계점에 도달할 때까지 조금씩 증가합니다).
- · 원점에서 시작하여 여러 r 값의 반지름 r에 대한 최소 예측 분산 그림.
- · v(x) = p에서의 수평선, 여기서 p는 적합할 모형 내 모수의 개수입니다. "최적" 설계는 최대 예측 분산이 설계 공간의 모든 점에서 p보다 작거나 같은 설계입니다.
VDG는 주어진 점에서 원점 또는 설계 중심까지의 거리를 나타내는 여러 r 값에서 척도화된 예측 분산의 평균, 최대값 및 최소값을 표시합니다.
VDG를 사용하여 설계의 다른 측면 평가
VDG를 사용하여 예측 분산의 관점에서 단일 설계의 성능을 평가할 수 있습니다. 또한 VDG를 사용하여 두 개 이상의 설계를 비교할 수 있습니다. 설계에 중심점을 추가하는 효과를 평가하기 위해서도 VDG를 사용할 수 있습니다.
또한 VDG를 사용하여 설계가 회전 가능한지 여부도 평가할 수 있습니다. 회전 가능한 설계에서는 그래프의 세 선(최소값, 평균, 최대값)이 모두 일치합니다. 최소값, 평균, 최대값이 일치하지 않는 경우에는 면 중심 설계를 회전할 수 없습니다.
Monte Carlo 시뮬레이션을 통해 예측 분산 추정
이 항목에서는 VDG에 표시되는 최소값, 최대값 및 평균 예측 분산을 추정하기 위해 사용되는 수학적 방법에 대해 설명합니다. 매크로를 실행하여 VDG를 표시하고 해석하는 방법만 보려면 이 항목을 건너뛰어도 됩니다.
앞에서 언급한 대로 반지름 값이 고정된 경우 최소값, 최대값 및 누적 척도화된 예측 분산을 찾으려면 검색을 수행해야 합니다. Minitab 매크로를 위해 선택된 방법은 Monte Carlo 시뮬레이션 및 설계의 중심 x = (0,0,…,0)T에서 같은 거리에 있는 점을 고르게 검색할 수 있는 능력을 기반으로 합니다.
원점으로부터 여러 거리에서 1) 최소 예측 분산, 2) 최대 예측 분산, 3) 누적 예측 분산 등 세 가지 양을 계산해야 합니다. 이러한 값을 찾는 데는 여러 가지 방법이 있습니다. 한 가지 방법은 비선형 프로그래밍 알고리즘을 사용하여 최소 및 최대 예측 분산을 찾는 것입니다. 그러나 여기서 이러한 값을 추정하기 위해 선택한 방법은 표본을 고르게 추출하고 여러 r 값에 대해 설계의 중심으로부터 같은 거리에 있는, 많은 고유점을 찾는 것입니다. 같은 거리에 있는 점들의 공간에서 다음 두 조건이 충족되면 최소 및 최대 예측 분산을 적절히 추정할 수 있습니다. 첫째, 같은 거리에 있는 점을 고르게 추출해야 하는데, 다시 말하면 특정 영역에서 다른 영역보다 같은 거리에 있는 점을 선택하지 않아야 합니다. 둘째, 점의 개수가 가능한 설계점의 전체 공간을 덮을 수 있을 만큼 충분히 커야 합니다.
표본 추출해야 하는 모든 점이 같은 거리에 있기 때문에 점을 추출하는 문제는 주어진 반지름에 대해 n-볼 또는 초구에서 점을 얻는 좋은 방법을 찾는 것과 같습니다.
이 절차는 Marsaglia(1972)에 설명되어 있으며 아래와 같이 요약할 수 있습니다.
- 예를 들어, 표준 정규 분포에서 정규 랜덤 변수의 n-차원 벡터를 생성합니다. 벡터를 x = (x1, x2,…,xn)로 설정합니다. 여러 벡터 x를 생성합니다.
- 생성한 모든 점 x에 대해 반지름 ρ를 계산합니다.

- 벡터 x의 각 항목에 r을 곱하여 1단계에서 구한 각각의 원래 설계점을 변환합니다. 여기서 r은 점을 추출할 초구의 반지름을 나타냅니다.
여기서는 반지름이 r인 초구의 점을 표본 추출하는 방법에 대해 설명했습니다. 이 표본 추출 방법을 사용하여 최대 또는 최소 예측 분산을 추정할 수 있습니다. 이 표본을 사용하면 n이 큰 경우 큰 수의 약한 법칙에서 추출된 설계점의 평균 예측 분산을 사용하여 실제 누적 예측 분산을 추정할 수 있습니다.
참고 문헌
[1] Marsaglia G. "Choosing a Point from the Surface of a Sphere". The Annals of Mathematical Statistics, Vol. 43, No. 2 (1972), pp. 645-646.
[2] Myers R, Montgomery D. (2002). Response Surface Methodology - Process and Product Optimization Using Designed Experiments, Second Edition. John Wiley & Sons, Inc.
