매크로 다운로드
Minitab에서 다운로드한 매크로의 위치를 지정해야 합니다. 을 선택합니다. 매크로 위치에서 매크로 파일 저장 위치로 이동합니다.
중요
기존 웹 브라우저를 사용하는 경우 다운로드 단추를 클릭하면 Minitab 매크로와 .mac 파일 확장자를 공유하는 Quicktime에서 해당 파일을 열 수 있습니다. 매크로를 저장하려면 다운로드 단추를 마우스 오른쪽 단추로 클릭하고 다른 이름으로 대상 저장을 선택합니다.
필수 입력
- 반응 데이터의 열
- 코드화되지 않은 요인 수준이 있는 해당 열
선택적 입력
- STORE C-C
- 가장 가파른 오르막/내리막 경로를 워크시트에 저장합니다. 입력은 경로가 저장될 워크시트의 열을 나타냅니다. 각 요인당 하나의 저장 열을 지정합니다. 이 하위 명령을 지정하지 않으면 경로가 표시되지만 해당 경로는 워크시트에 저장되지 않습니다.
- STEP K
- 공정 변수의 단계 크기 또는 증분(
 )을 코드화된 단위로 정의합니다. 기본적으로 증분은 1입니다.
)을 코드화된 단위로 정의합니다. 기본적으로 증분은 1입니다. - BASE C
- 가장 가파른 오르막/내리막 경로의 단계 크기를 정의합니다. 입력 b는 단계 크기를 정의하는 계수가 있는 열입니다. 기본적으로 단계 크기는 절대값이 가장 큰 요인 계수입니다.
- DESCENT
- 가장 가파른 오르막 경로(기본값) 대신 가장 가파른 내리막 경로를 계산하기 위해 지정합니다.
- RUNS K
- 생성할 런 수를 나타냅니다. 입력값 r은 상수입니다. 기본적으로 런 수는 5입니다.
매크로 실행
2-요인 설계에서 요인이 C5와 C6에 저장되어 있고, 반응이 C7에 있다고 가정합니다. 잠재적으로 반응을 최대화하는 경로를 찾으려고 합니다. 또한 이 경로를 워크시트의 C9-C10 열에 저장하려고 하며 런 사이의 단계 크기는 (코드화된 단위로) 2여야 하고 C5에 포함된 요인이 기본 요인이 됩니다. 마지막으로 가장 가파른 오르막 경로를 따라 8개의 런을 계산하려고 합니다.
%ASCENT C7 C5-C6;
STORE C9-C10;
STEP 2;
BASE C5;
RUNS 8.실행을(를) 클릭합니다.
추가 정보
반응 표면 방법의 개요
반응 표면 방법(RSM)을 사용하면 제어 가능한 요인에 대한 최적의 설정을 결정하여 관심의 대상이 되는 반응을 최적화할 수 있습니다. 따라서 RSM의 기본 목표는 최적의 설정을 찾는 것입니다  .
.
순차적 실험을 사용하여 이 작업을 수행할 수 있습니다. 일반적으로 요인 또는 부분 요인 설계로 시작하여 관련이 없는 요인을 제외합니다. 반응에 대한 회귀 모형을 지정한 후 가장 가파른 경로를 따라 추정하고 실험하여 반응을 최대화합니다. 마지막으로 반응 표면 설계를 선택하여 곡면성을 모형화하고 최적의 반응을 찾습니다.
RSM의 세 가지 기본 단계는 다음과 같습니다.
- 선별 실험의 요인을 식별합니다.
- 가장 가파른 오르막/내리막 경로를 따릅니다.
- 2차 회귀 모형을 적합하고 최적화합니다.
다음 섹션에서는 가장 가파른 경로 및 경로를 계산하는 방법에 대해 설명하며, 두 개의 예를 통해 이 작업을 수행하기 위한 Minitab 매크로를 제공합니다.
가장 가파른 오르막/내리막 경로의 정의
선별 실험을 수행하고 주효과만 사용하여 반응의 선형 모형을 구한 후 반응을 신속하게 개선하는 방향으로 이동할 수 있습니다. 반응을 최대화하려면 가장 가파른 오르막 경로를 따릅니다. 반응을 최소화하려면 가장 가파른 내리막 경로를 따릅니다.
가장 가파른 오르막/내리막 경로 계산
가장 가파른 경로를 계산하려면 먼저 모형을 적합해야 합니다. 실험에 두 개의 요인이 있고 요인 x1과 x2 사이의 교호작용이 유의하지 않다고 가정합니다. 이 실험에 대한 모형 방정식은 다음과 같습니다.
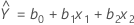
설명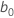 은 절편 추정치이고
은 절편 추정치이고 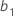 ,
, 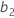 는 각각 요인
는 각각 요인  및
및 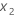 에 대한 계수입니다.
에 대한 계수입니다.
모형 방정식을 구한 후:
- 하나의 공정 변수를 "기본 요인"으로 선택하고 기본 요인에 대한 단계 크기 또는 증분(
 ) i를 식별합니다.
) i를 식별합니다.
참고
기본적으로 기본 요인이 지정되지 않은 경우 매크로가 회귀 계수의 최대 절대값을 가진 변수를 선택합니다.
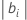 .
. - 다음 방정식을 사용하여 다른 공정 변수의 증분을 계산합니다.
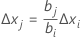
- 증분을 코드화된 단위에서 코드화되지 않은 단위로 변환합니다.
Quality Companion의 가장 가파른 오르막 형식
Quality Companion 2의 표준 형태를 사용하여 가장 가파른 오르막/내리막 경로를 계산할 수도 있습니다. 기본 변수, 코드화되지 않은 요인 수준, 증분을 지정하고 원하는 수의 런을 추가하여 입력 모수를 입력합니다.
예 1: 에칭 비율 최대화
다음 예는 Myers and Montgomery의 Response Surface Methodology: Process and Product Optimization Using Designed Experiments에 있는 예를 사용자 정의한 것입니다.
반도체 제조에서 목표는 요인 양극-음극 차이(차이) 및 음극의 동력(동력) 수준에 변화를 주어 플라스마 에칭 비율(반응)을 최대화하는 것입니다. 실험 수행 결과 다음 모형이 생성된다고 가정합니다.
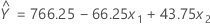
여기서  은 차이를 나타내고
은 차이를 나타내고 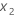 는 동력을 나타냅니다.
는 동력을 나타냅니다.
매크로를 사용하여 가장 가파른 오르막 경로를 계산하려면 먼저 워크시트에서 코드화되지 않은 단위의 반응과 주효과( 및
및 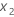 )에 해당하는 열을 나타냅니다. 이 예의 경우 반응(에칭 비율)은 C7, 주효과(차이, 동력)는 C5와 C6에 있습니다.
)에 해당하는 열을 나타냅니다. 이 예의 경우 반응(에칭 비율)은 C7, 주효과(차이, 동력)는 C5와 C6에 있습니다.
매크로를 실행하려면 로 이동하고 다음을 입력합니다.
%ASCENT C7 C5-C6;
STORE C9-C10.참고
매크로의 ASCENT17.mac 버전을 사용하는 경우 %ASCENT 대신 %ASCENT17을 사용합니다.
명령 제출을 클릭합니다.
Minitab에서는 워크시트의 데이터를 사용하여 가장 가파른 오르막 경로에 5개의 런을 만들어 C9 및 C10 열에 경로를 저장합니다. 최종 모형에 두 개의 요인만 있는 경우 산점도를 만들어 가장 가파른 오르막/내리막 경로를 표시할 수 있습니다.
예 2: 반응 수율 최소화
이 예는 Myers and Montgomery가 가장 가파른 오르막 경로 대신 가장 가파른 내리막 경로를 사용하기 위해 만든 예를 사용자 정의한 것입니다.
실험의 목표가 A(반응 물질 A의 양), B(반응 시간), C(반응 물질 C의 양), D(온도) 등 제어 가능한 네 가지 요인의 더 낮은 설정을 찾아 반응 수율을 최소화하는 것이라고 가정합니다. 네 가지 요인의 코드화되지 않은 (자연) 수준은 10, 15그램(요인 A), 1, 2분(요인 B), 25, 35그램(요인 C), 75, 85°C(요인 D)입니다. 또한 기본 계수는 반응 물질 A에 해당하며 단계 크기는 코드화되지 않은 단위로 1그램입니다. 적합 모형은 다음과 같습니다.
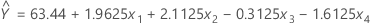
매크로를 사용하여 가장 가파른 내리막 경로를 계산하려면 하위 명령 DESCENT를 사용합니다. 반응 물질 A에 해당하는 열이 C5이기 때문에 BASE에 대한 입력은 C5입니다. 코드화된 단위의 STEP은 요인 A의 코드화된 한 단위가 2.5과 같기 때문에 1/2.5 = 0.4입니다. 매크로를 실행하려면 로 이동하고 다음을 입력합니다.
%ASCENT C9 C5-C8;
STORE C11-C14;
STEP 0.4;
BASE C5;
DESCENT;
RUNS 10.참고
매크로의 ASCENT17.mac 버전을 사용하는 경우 %ASCENT 대신 %ASCENT17을 사용합니다.
참고
교과서의 원래 예에 대한 출력을 구하려면 가장 가파른 오르막 경로를 사용하여 개선 방향을 계산합니다. 아래와 같이 DESCENT 하위 명령 없이 명령 블럭을 제출합니다.
%ASCENT C9 C5-C8;
STORE C11-C14;
STEP 0.4;
BASE C5;
RUNS 10.참고 문헌
R. Myers and D. Montgomery (2002). Response Surface Methodology - Process and Product Optimization Using Designed Experiments, Second Edition. John Wiley & Sons, Inc.
