매크로 다운로드
Minitab에서 다운로드한 매크로의 위치를 지정해야 합니다. 을 선택합니다. 매크로 위치에서 매크로 파일 저장 위치로 이동합니다.
중요
기존 웹 브라우저를 사용하는 경우 다운로드 단추를 클릭하면 Minitab 매크로와 .mac 파일 확장자를 공유하는 Quicktime에서 해당 파일을 열 수 있습니다. 매크로를 저장하려면 다운로드 단추를 마우스 오른쪽 단추로 클릭하고 다른 이름으로 대상 저장을 선택합니다.
필수 입력
- 숫자 반응 데이터의 열
- 요인 수준의 해당 열
참고
UNSTACKED 하위 명령을 사용하여 분할 데이터를 사용할 수 있습니다.
선택적 입력
- UNSTACKED
- 데이터가 분할되어 있는지 여부를 지정합니다.
- FALPHA
- 원하는 모임 알파 수준(기본값 0.20)을 지정하는 데 사용됩니다.
- CONTROL C
- 제어할 열(C)을 지정하는 데 사용됩니다.
참고
데이터가 쌓여 있는 경우, 제어 그룹에 대한 반응은 다른 요인 수준에 대한 반응과 같은 열에 있지 않아야 합니다. 제어 그룹에 대한 반응은 별도의 열에 있어야 합니다.
매크로 실행
반응 데이터가 C1에 있고 요인 수준이 C2에 있다고 가정합니다. 매크로를 실행하려면 을 선택하고 다음을 입력합니다.
%KRUSMC C1 C2실행을(를) 클릭합니다.
결과
결과의 첫 번째 부분에는 수행하는 비교의 수(k),
 , 모임 알파(α), Bonferroni 개별 알파(β),
, 모임 알파(α), Bonferroni 개별 알파(β),  , 양측 임계 z-값이 표시됩니다.
, 양측 임계 z-값이 표시됩니다.
다음 섹션에는 표준화된 그룹 평균 순위 차이(θ) 및 이러한 차이와 연관된 p-값이 표시됩니다. 이러한 표는 대칭이기 때문에 표의 위쪽 삼각형 부분에 별표가 있습니다. 또한 대각선이 한 그룹과 그룹 자체 간의 비교를 나타내기 때문에 표의 대각선 아래에 0이 있습니다(이러한 비교는 무의미하며 분석에서 고려되지 않습니다). 이 예를 읽는 방법의 예는 다음과 같습니다: 그룹 2와 4 사이에는 어떤 차이가 있습니까? 세 번째 섹션에는 중위수의 부호 신뢰 구간이 표시됩니다. 이러한 구간의 신뢰 수준은 모임 알파에서 제어됩니다. 이러한 구간은 전체 모임 알파에서 제어되기 때문에 쌍으로 비교할 수 있습니다(부록 2). 전체 또는 일부 구간에 대해 원하는 신뢰 수준을 달성하지 못할 수도 있음을 명심해야 합니다. 또한 표본 크기가 다른 경우 모임 알파에 의한 "전체" 범위가 정확하지 않지만, 종종 합리적인 근사입니다.
마지막 섹션에는 "유의한" 차이가 표시됩니다(있는 경우). 이 섹션에는 z-값, 임계 z-값, z-값과 연관된 p-값이 표시됩니다.
그래프에는 비절대 그룹 평균 순위 표준화 차이가 표시합니다. 이 그래프는 그룹 차이의 크기뿐만 아니라 방향도 볼 수 있기 때문에 매우 유용합니다. 또한 양수 및 음수 임계 z-값이 표시되기 때문에 차이가 "유의"한지 여부를 알 수 있습니다.
데이터의 같은 값
데이터에 같은 값이 있는 경우 불편화 상수(수정 요인) 2가 계산됩니다. 그런 다음 H 통계량이 3으로 수정되고, 표준 편차(ξ) 역시 이 수정 요인 4에 의해 수정되며, 결과에는 수정된 표와 수정되지 않은 표가 모두 표시됩니다. 표준 편차(ξ) 역시 이 수정 요인 4에 의해 수정됩니다 세션 창 결과에는 수정된 표와 수정되지 않은 표가 모두 표시됩니다. 수정되지 않은 표를 표시하는 주된 이유는 같은 값이 z-값에 미치는 영향을 보여주기 위한 것입니다. 같은 값이 아주 광범위한 경우, 이러한 검정에서 분포가 계량형이라고 가정하기 때문에 데이터의 유효성을 확인해야 합니다. 같은 값은 대부분 결론에 거의 또는 전혀 영향을 미치지 않습니다.
감사의 말씀
펜실베니아 주립대학교 Tom Hettmansperger 박사님의 매크로 검토, 이 작업과 관련된 다양한 토론, 박사님의 귀중한 시간과 수고에 대해 감사드립니다. 또한 Nicholas Bolgiano씨와 Mike Delozier씨(Minitab, Inc.)의 매크로 관련 의견 및 제안에 대해 감사드립니다.
추가 정보
Dunn의 검정
쌍체 동시 추론을 효과적으로 수행하는 방법은 Dunn에 의해 소개되었습니다(1964). 먼저 데이터를 조합하고, 순위를 매기고, 그룹 평균 순위를 찾은 다음, 이러한 평균 순위의 표준화된 절대 차이를 사용합니다.
다음과 같이 설정합니다. k = 처리의 수, 
다음과 같이 설정합니다. 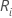 = i번째 처리에 대한 순위의 합, i = 1,…,k
= i번째 처리에 대한 순위의 합, i = 1,…,k
다음과 같이 설정합니다. 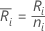
여기서 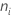 = i번째 처리에 대한 관측치의 수
= i번째 처리에 대한 관측치의 수
다음과 같이 설정합니다. 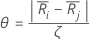
여기서 j=l,...,k 및 j  i
i
여기서 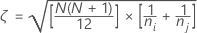
H 통계량
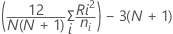
여기서 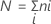
그러면 다음과 같은 경우 "유의성"을 선언합니다.

여기서 
여기서 α는 지정된 모임 알파 값입니다. 
