Fisher의 정확 검정
Fisher의 정확 검정은 독립성 검정입니다. 이 검정은 Pearson 및 우도 비 검정에 사용되는 근사 카이-제곱 분포가 아니라 정확한 분포를 기반으로 합니다. Fisher의 정확 검정은 기대 셀 카운트가 낮고 카이-제곱 근사가 매우 좋지 않을 때 유용합니다.
수식
- 모집단 크기
- 총 관측치 수
- 모집단 내 성공 횟수
- 첫 번째 행의 관측치 수
- 표본 크기
- 첫 번째 열의 관측치 수
예제
| 어린이 | 성인 | 행 합계 | |
|---|---|---|---|
| 당분 | 9 | 1 | 10 |
| 초콜릿 칩 | 2 | 8 | 10 |
| 열 합계 | 11 | 9 | 20 |
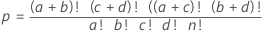
| 어린이 | 성인 | 행 합계 | |
|---|---|---|---|
| 당분 | a | b | a+b |
| 초콜릿 칩 | c | d | c+d |
| 열 합계 | a+c | b+d | a+b+c+d |
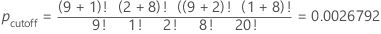
이 예제의 경우 다른 가능한 행렬에 대한 pcutoff보다 작거나 같은 p-값의 합이 0.0054775입니다.
McNemar의 정확 검정
McNemar의 검정은 처리 전과 후에 관측된 비율을 비교합니다. 예를 들어, McNemar의 검정을 사용하여 교육 프로그램이 질문에 정답을 맞추는 참가자의 비율을 변화시키는지 여부를 확인할 수 있습니다.
McNemar의 검정에 대한 관측치는 아래 표시된 것과 같이 2x2 표로 요약할 수 있습니다.
| 처리 후 | |||
| 처리 전 | 조건 참 | 조건 참이 아님 | 합계 |
| 조건 참 | n11 | n12 | n1. |
| 조건 참이 아님 | n21 | n22 | n2. |
| 합계 | n·1 | n·2 | n·· |
교육 예에 대한 조건은 정답입니다. 따라서 n21은 교육 전이 아니라 교육 후에 질문에 올바르게 대답하는 참가자의 수를 나타냅니다. 그리고 n12는 교육 후가 아니라 교육 전에 질문에 올바르게 대답하는 참가자의 수를 나타냅니다. 총 참가자 수는 n..으로 나타냅니다.
추정된 차이
δ를 모집단의 주변 확률 p1.- p.1 간의 차이로 설정합니다. 추정된 차이  는 다음 공식으로 계산됩니다.
는 다음 공식으로 계산됩니다.
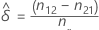
신뢰 구간
근사적인 100(1 – α)% 신뢰 구간은 다음 공식으로 계산됩니다.

여기서 α는 검정에 대한 유의 수준 z α/2는 α/2의 꼬리 확률과 연관된 z-점수이며, SE는 다음 공식으로 계산됩니다.
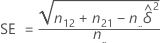
p-값
귀무 가설은 δ = 0입니다. 귀무 가설의 검정에 대한 정확한 p-값은 다음과 같이 계산됩니다.

여기서 X는 사건 확률이 0.5이고 시행 횟수가 n21 + n12와 같은 이항 분포에서 추출된 랜덤 변수입니다.
Cochran-Mantel-Haenszel 검정
이 검정에서는 3차 교호작용이 존재하지 않는다고 가정합니다. 검정의 목적은 방해 요인을 제어하는 동안 두 변수 사이의 관계를 평가하는 것입니다. CMH 통계량은 자유도가 1인 카이-제곱 백분위수와 비교됩니다.
Cochran-Mantel-Haenszel(CMH) 검정은 세 개 이상의 분류 변수가 존재하고 처음 두 변수의 수준 수가 각각 2개인 경우에만 적용됩니다. 처음 두 변수 이외의 모든 변수는 CMH 검정의 목적상 단일 변수 Z로 간주되며, 각 수준 조합이 Z 수준으로 간주됩니다.
공식
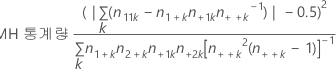
표기법
| 용어 | 설명 |
|---|---|
| k | Z 수준 |
| n11k | 첫 번째 행, 첫 번째 열의 관측치 수 |
| n1+k | 첫 번째 행의 관측치 수 |
| n+1k | 첫 번째 열의 관측치 수 |
| n++k | 총 관측치 수 |
| n2+k | 두 번째 행의 관측치 수 |
| n+2k | 두 번째 열의 관측치 수 |
