원하는 방법 또는 공식을 선택하십시오.
이 항목의 내용
Pearson의 r
Pearson의 상관 계수는 두 변수 간 선형 관계의 측도이며, 범위는 +1에서 -1 사이입니다. 상관 계수가 +1이면 두 변수 간에 완벽한 양의 선형 관계가 있음을 나타냅니다.
데이터는 데이터 값을 취하고 간격이 동일한 정수로 코드화하여 순서형으로 변환됩니다. 예를 들어 계열 4, 7, 20은 1, 2, 3으로 분석되며 계열 4, 7, 7, 20은 1, 2, 2, 3으로 분석됩니다.
참고
이 통계량은 동일한 시퀀스 4, 7, 7, 20을 1, 2.5, 2.5, 3으로 분석하는 Spearman 통계량과 다릅니다.
공식
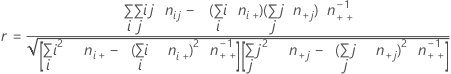
표기법
| 용어 | 설명 |
|---|---|
| ni+ | i번째 행의 관측치 수 |
| n+j | j번째 열의 관측치 수 |
| nij | i번째 행과 j번째 열에 해당하는 셀의 관측치 |
| n++ | 총 관측치 수 |
Spearman의 로
Spearman의 로는 두 변수의 선형 관계에 대한 측도입니다. Spearman의 상관 계수는 숫자가 순위로 변환된 후에만 계산되기 때문에만 Pearson의 상관 계수와 다릅니다.
공식
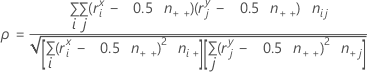
i = 1인 경우:

i = 2, 3,..., r인 경우:
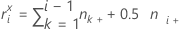
j = 1인 경우:

j = 2, 3,..., c인 경우:
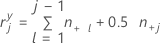
표기법
| 용어 | 설명 |
|---|---|
| c | 열 수 |
| r | 행 수 |
| ni+ | i번째 행의 관측치 수 |
| n+j | j번째 열의 관측치 수 |
| nij | i번째 행과 j번째 열에 해당하는 셀의 관측치 |
| n++ | 총 관측치 수 |
