원하는 방법 또는 공식을 선택하십시오.
각 범주에 대한 기대값
공식
각 범주 i에 대한 기대값 E는 다음과 같이 계산됩니다.
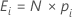
표기법
| 용어 | 설명 |
|---|---|
| pi | i번째 범주에 대한 검정 비율(1/k 또는 사용자가 제공하는 값과 같음) |
| k | 구별 범주의 수 |
| N | 총 관측값(O1 + ... + Ok) |
| Oi | i번째 범주에 대한 관측값 |
카이-제곱 검정 통계량
공식
카이-제곱 검정 통계량은 다음과 같이 계산됩니다.
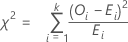
표기법
| 용어 | 설명 |
|---|---|
| k | 구별 범주의 수 |
| Oi | i번째 범주에 대한 관측값 |
| Ei | i번째 범주에 대한 기대값 |
카이-제곱 통계량에 대한 기여도
공식
i번째 범주의 카이-제곱 값에 대한 기여도는 다음과 같습니다.

표기법
| 용어 | 설명 |
|---|---|
| Oi | i번째 범주에 대한 관측값 |
| Ei | i번째 범주에 대한 기대값 |
자유도(DF)
공식
자유도(DF)는 다음과 같이 계산됩니다.

표기법
| 용어 | 설명 |
|---|---|
| DF | 자유도 |
| k | 범주 수 |
p-값
공식
p-값은 Prob (Χ > 검정 통계량)으로 계산됩니다.
표기법
| 용어 | 설명 |
|---|---|
| X | 자유도가 k – 1인 카이-제곱 분포를 따릅니다. |
계산 예
주어진 값:
| 범주 i | 관측된 Oi | 검정 비율 pi |
|---|---|---|
| A | 5 | 0.1 |
| B | 15 | 0.2 |
| C | 10 | 0.3 |
| D | 10 | 0.4 |
| N=40 |
계산된 값:
| 범주 i | 기대값
Ei = (pi * N) |
카이-제곱에 대한 기여도
(Oi- Ei)2 / Ei |
|---|---|---|
| A | 0.1 * 40 = 4 | (5 – 4)2 / 4 = 0.25 |
| B | 0.2 * 40 = 8 | (15 – 8)2 / 8 = 6.125 |
| C | 0.3 * 40 = 12 | (10 – 12)2 / 12 = 0.3333 |
| D | 0.4 * 40 = 16 | (10 – 16)2 / 16 = 2.25 |
χ2 = 0.2500 + 6.1250 + 2.2500 + 0.3333 = 8.9583
DF = k – 1 = 3
p-값 = Prob (Χ > 8.9583) = 0.0299
표기법
| 용어 | 설명 |
|---|---|
| DF | 자유도 |
| k | 범주 수 |
