이 항목의 내용
1단계: 계산된 값 조사
Minitab에서는 사용자가 입력한 세 검정력 함수 변수의 값을 사용하여 반복실험 횟수, 효과 크기, 설계의 검정력 또는 중앙점의 수를 계산합니다.
- 효과
-
반복실험 횟수, 검정력 값, 중앙점 수를 입력하면 Minitab에서 효과를 계산합니다. 효과는 설계에서 탐지하려는 요인의 높은 수준과 낮은 수준 간 반응의 차이입니다. 이 차이는 한 요인(주효과)만의 결과입니다.
- 중앙점
-
반복실험 횟수, 효과 크기, 검정력 값을 입력하면 Minitab에서 중앙점 수를 계산합니다. 중앙점은 모든 요인 수준이 낮은 수준과 높은 수준 사이의 중간으로 설정된 실험 런입니다. 중앙점은 주로 곡면성 효과를 탐지하기 위해 사용되지만, 중앙점을 추가하면 검정력이 어느 정도 증가할 수도 있습니다.
- 반복실험
- 효과 크기, 검정력 값, 중앙점 수를 입력하면 Minitab에서 반복실험 횟수를 계산합니다. 반복실험은 동일한 요인 설정을 가진 복수 실험 런입니다. 반복실험 횟수가 정수 값이므로 실제 검정력은 목표치보다 약간 클 수도 있습니다.
- 전체 런 수
- 모든 경우 Minitab은 반복실험 횟수와 중앙점의 수에서 전체 런 수를 계산합니다. 전체 런 수는 구석점 수와 반복실험 횟수의 곱에 중앙점의 수를 더한 값입니다.
- 검정력 값
- 효과 크기, 검정력 값, 중앙점 수를 입력하면 Minitab에서 반복실험 횟수를 계산합니다. 검정력은 유의한 효과를 올바르게 찾을 확률입니다. 일반적으로 0.9의 검정력 값이 충분한 것으로 간주됩니다. 0.9의 값은 효과를 탐지할 확률이 90%라는 것을 나타냅니다. 일반적으로 전체 런 수가 더 작거나 효과가 더 작은 경우 설계의 검정력이 더 낮습니다.
방법
| 요인: | 15 | 설계: | 32 |
|---|---|---|---|
| 중앙점(전체): | 0 |
결과
| 중앙점 | 효과 | 반복 | 전체 런 수 | 목표 검정력 | 실제 검정력 |
|---|---|---|---|---|---|
| 0 | 2.0 | 1 | 32 | 0.8 | 0.877445 |
| 0 | 2.0 | 2 | 64 | 0.9 | 0.995974 |
| 0 | 0.9 | 4 | 128 | 0.8 | 0.843529 |
| 0 | 0.9 | 5 | 160 | 0.9 | 0.914018 |
주요 결과: 중앙점, 효과, 반복실험, 전체 런 수, 목표 검정력, 실제 검정력
이 결과에서 Minitab은 목표 검정력에 도달하기 위한 반복실험 횟수를 계산합니다. 0.8의 검정력으로 2의 효과를 탐지하는 설계에는 1번의 반복실험이 필요합니다. 0.9의 검정력을 달성하려면 설계에 2번의 반복실험이 필요합니다. 2번의 반복실험의 실제 검정력은 0.99보다 큽니다. 이 실제 검정력은 0.9보다 크거나 같고 정수의 반복실험 횟수를 사용하여 얻을 수 있는 가장 작은 검정력 값입니다. 0.8의 검정력으로 0.9의 더 작은 효과를 탐지하려면 설계에 4번의 반복실험이 필요합니다. 0.9의 검정력으로 0.9의 더 작은 효과를 탐지하려면 설계에 5번의 반복실험이 필요합니다.
2단계: 검정력 곡선 조사
설계에 적절한 속성을 평가하려면 검정력 곡선을 사용합니다.
검정력 곡선은 중앙점과 반복실험의 모든 조합에 대한 검정력과 효과 크기의 관계를 나타냅니다. 검정력 곡선의 각 기호는 사용자가 입력하는 속성을 기준으로 계산된 값을 나타냅니다. 예를 들어, 반복실험 횟수, 검정력 값과 중앙점 수를 입력하면 Minitab에서 반복실험과 중앙점의 조합에 해당하는 효과 크기를 계산하고 계산된 값을 그래프에 표시합니다. 반복실험이나 중앙점을 계산하면 목표 검정력을 달성하는 조합에 있는 반복실험과 중앙점의 다른 조합에 대한 곡선도 그래프에 포함됩니다. 통계적 유의성을 평가하기에 자유도가 충분하지 않은 경우에 대해서는 그래프에 곡선이 표시되지 않습니다.
곡선의 값을 조사하여 특정한 검정력 값, 구석점 수 및 중앙점 수에서 실험이 탐지하는 효과 크기를 확인합니다. 일반적으로 0.9의 검정력 값이 적절한 것으로 간주됩니다. 그러나 일부 실무자들은 0.8의 검정력 값이 적절하다고 생각합니다. 설계의 검정력이 낮은 경우 실제적으로 유의한 효과를 탐지하지 못할 수도 있습니다. 반복실험 횟수를 늘리면 설계의 검정력이 증가합니다. 설계에 적절한 검정력을 달성하기에 충분한 수의 실험 런이 필요합니다. 설계에서 작은 크기보다 큰 크기를 탐지하기 위한 검정력이 더 높습니다.
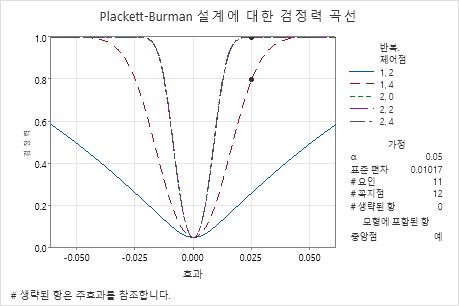
이 결과에서 Minitab은 0.025의 효과 크기에 대해 0.8 또는 0.9 이상의 목표 검정력을 달성하기 위한 반복실험 횟수를 계산합니다. 설계된 실험에는 11개의 요인을 조사하기 위해 12개의 구석점이 있습니다. 계산에서는 블럭당 중앙점이 0개, 2개 또는 4개인 실험된 설계를 고려합니다. 1번의 반복실험과 4개의 중앙점을 보여주는 곡선에는 검정력이 목표 검정력 0.8보다 큰 위치에 0.25의 효과에 대한 기호가 있습니다. 2번의 반복실험이 있는 실험을 나타내는 3개의 곡선에는 0.025의 효과를 탐지하기 위한 검정력이 0.9의 목표 검정력보다 크다는 것을 보여줍니다.
반복실험이 2번이고 중앙점이 2개인 솔루션이 존재하고 반복실험이 1번이고 중앙점이 4개인 솔루션이 존재하기 때문에 그래프에는 반복실험이 1번이고 중앙점이 2개인 실험에 대한 곡선도 포함됩니다. 이 실험은 0.025의 효과에 대한 목표 검정력을 달성하지 못하므로 기호가 없습니다. 이 실험은 모형에서 항이 제외되지 않을 때 통계적 유의성을 평가하기에 자유도가 충분하지 않기 때문에 반복실험이 1번이고 중앙점이 0개인 실험에 대한 곡선이 그래프에 포함되지 않습니다.
