원하는 방법 또는 공식을 선택하십시오.
이 항목의 내용
검정력 계산
수식
이 계산은 비중심 모수가 λ인 F-분포를 기반으로 합니다.
비중심 모수
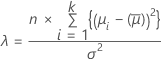
검정력

Minitab에서는 다른 평균이 모두 최소값과 최대값의 중간에 있다는 최악의 가정 하에 λ를 계산합니다. 결과는 지정된 표본 크기와 지정된 평균 간의 최대 차이에 대해 검정력을 최소화하는 평균의 구성입니다.
표기법
| 용어 | 설명 |
|---|---|
| k | 수준 수 |
| n | 각 수준의 표본 수 |
| α | 유의 수준 |
| σ | 표준 편차 |
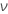 | 오차에 대한 자유도, k * ( n – 1 )와 같음 |
| fα | 임계값(자유도가 k – 1 및 ν인 F 분포의 상한 α 점) |
| μi | 수준 i에서의 평균 반응 |
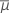 | 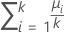 합계 (μi) / k 합계 (μi) / k |
 | fα에서 평가된 자유도가 k – 1, 분모 자유도가 v, 비중심 모수가 λ인 F 분포의 CDF |
표본 크기 및 최대 차이 계산
공식
검정력과 표본 크기 값을 제공하면 Minitab에서 최대 차이 값을 계산합니다. 검정력과 최대 차이 값을 제공하면 Minitab에서 표본 크기 값을 계산합니다.
이 두 경우에 Minitab에서는 검정력 방정식과 함께 반복 알고리즘을 사용합니다. 각 반복에서 Minitab은 시험 표본 크기 또는 시험 차이에 대한 검정력을 평가하고 사용자가 지정한 값에 도달하면 중지합니다.
목표 검정력 및 실제 검정력
Minitab에서 표본 크기를 계산할 때 목표 검정력을 생성하는 표본 크기에 해당하는 정수 값이 없을 수도 있습니다. 이 경우 Minitab에서는 목표 검정력 값을 실제 검정력 옆에 표시합니다. 실제 검정력은 정수 표본 크기에 해당하고 목표값에 가장 가깝지만 목표값보다 큰 값입니다.
