Mann-Whitney 검정에 대한 방법 및 공식

원하는 방법 또는 공식을 선택하십시오.

이 항목의 내용

검정 통계량
같은 값 순위매기기
p-값
점 추정치
신뢰 구간

검정 통계량

Minitab에서는 Mann-Whitney 통계량을 다음과 같이 계산합니다.

두 결합된 표본에 순위를 매깁니다. Minitab에서는 가장 작은 관측치에 순위 1을 지정하고 두 번째로 작은 관측치에 순위 2를 지정하며, 이런 방식으로 계속합니다.
둘 이상의 관측치가 같은 경우 Minitab에서는 두 관측치에 모두 평균 순위를 지정합니다.
첫 번째 표본의 순위를 합합니다.

같은 값 순위매기기

같은 값은 두 개 이상의 관측치가 같을 때 발생합니다. 데이터에 같은 값이 있는 경우, Minitab에서는 다음과 같이 데이터에 순위를 매깁니다.

괸측치를 오름차순으로 정렬합니다.
같은 값이 없는 것처럼 각 관측치에 순위를 지정합니다.
같은 값의 집합인 경우, 해당하는 순위의 평균을 계산하여 이 값을 해당 집합에 있는 각 같은 값에 새 순위로 지정합니다.

예

표본에는 2.4, 5.3, 2.4, 4.0, 1.2, 3.6, 4.0, 4.3, 4.0의 9개 관측치가 있습니다.

	관측치	순위 (같은 값이 없는 것으로 가정)	순위
	1.2	1	1
같은 값	2.4	2	2.5
같은 값	2.4	3	2.5
	3.6	4	4
같은 값	4.0	5	6
	4.0	6	6
	4.0	7	6
	4.3	8	8
	5.3	9	9

Mintab에서는 검정 통계량을 계산할 경우에도 다음 정보를 사용합니다.

같은 값의 집합 수 = 2
첫 번째 집합에 있는 같은 값의 수 = 2
두 번째 집합에 있는 같은 값의 수 = 3

p-값

공식

Mann-Whitney 검정에서는 정규 근사 방법을 사용하여 검정의 p-값을 결정합니다.

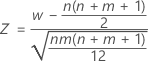는 근사적으로 평균이 0이고 표준 편차가 1인 정규 분포 N(0,1)를 따릅니다.

세 대립 가설의 정규 근사 p-값은 0.5의 연속성 수정을 사용합니다.

대립 가설	p-값
H₁: η₁ > η₂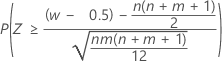
H₁: η₁ < η₂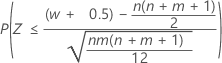
H₁: η₁ ≠ η₂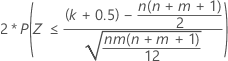

데이터에 같은 값이 있는 경우 Minitab에서는 위 Z 통계량의 분모를 다음으로 대치하여 p-값을 수정합니다.

수정된 p-값은 일반적으로 수정되지 않은 p-값보다 더 정확합니다. 그러나 수정되지 않은 p-값은 특정한 표본 쌍에 대해 수정된 p-값보다 항상 크기 때문에 더 보수적인 추정치입니다.

표기법

용어	설명
W	Mann-Whitney 검정 통계량
n	표본 1의 크기
m	표본 2의 크기
η₁	표본 1의 중위수
η₂	표본 2의 중위수
k
i	1, 2, …, I
I	같은 값의 집합 수
t_i	i 번째 같은 값 집합의 같은 값 수

점 추정치

Minitab에서 η₁ – η₂의 점 추정치를 계산하기 위해 사용하는 근사 알고리즘은 다음 문서에 설명되어 있습니다. J.W. McKean and T.A. Ryan, Jr. (1977). "An Algorithm for Obtaining Confidence Intervals and Point Estimates Based on Ranks in the Two Sample Location Problem", Transactions on Mathematical Software, 183–185.

신뢰 구간

η₁ – η₂의 신뢰 구간은 귀무 가설이 기각되지 않는 η₁ – η₂ 값의 범위로 정의됩니다.

Minitab에서 신뢰 구간을 계산하기 위해 사용하는 방법은 다음 문서에 설명되어 있습니다. J.W. McKean and T.A. Ryan, Jr. (1977). "An Algorithm for Obtaining Confidence Intervals and Point Estimates Based on Ranks in the Two Sample Location Problem", Transactions on Mathematical Software, pp.183-185.