이 항목의 내용
S
검정 통계량은 연관된 자유도가 (k - 1)인 근사 카이-제곱(χ2) 분포를 갖습니다. 하나 이상의 블럭 내 데이터에 같은 값이 있는 경우, Minitab에서는 평균 순위를 사용하여 같은 값에 대해 수정된 검정 통계량을 출력합니다. 이 방법에 대한 자세한 내용은 M. Hollander and D.A. Wolfe (1973)1를 참조하십시오.
공식
Minitab에서는 카이-제곱 검정 통계량을 계산하기 위해 각 블럭 내에서 개별적으로 데이터에 순위를 매기고 각 처리에 대해 순위를 합합니다.
데이터에 같은 값이 없는 경우 공식은 다음과 같습니다.
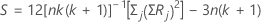
데이터에 같은 값이 있는 경우 공식은 다음과 같습니다.

여기서 C는 수정 요인으로, 다음과 같습니다.
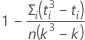
표기법
| 용어 | 설명 |
|---|---|
| j | 1, 2, ..., k |
| k | 처리 조건 수 |
| n | 블럭 수 |
| Rj | 처리 j에 대한 순위의 합 |
| i | 1, 2, ..., m |
| m | 같은 값의 집합 수 |
| ti | i번째 같은 값 집합의 같은 점수 수 |
- M. Hollander and D.A. Wolfe (1973). Nonparametric Statistical Methods, John Wiley & Sons, Inc.
총 중위수
처리 효과, 블럭 중위수 및 총 중위수를 계산하는 방법을 이해하려면 다음 데이터를 고려하십시오.
| 블럭 | ||||
| 처리 | 1 | 2 | 3 | 4 |
| 1 | 0.15 | 0.26 | 0.23 | 0.99 |
| 2 | 0.55 | 0.26 | −0.22 | 0.99 |
| 3 | 0.55 | 0.66 | 0.77 | 0.99 |
처리 효과를 계산하려면(Doksum 방법1) 먼저 처리 쌍 간의 차이의 중위수를 찾으십시오. 처리 1 - 처리 2에 대한 데이터 쌍들의 차이는 0.15 - 0.55 = −0.4, 0.26 – 0.26 = 0, 0.23 – (−0.22) = 0.45, 0.99 – 0.99 = 0입니다. 차이의 중위수는 0입니다. 다른 두 쌍에 대해 이 계산을 수행하면 처리 1 - 처리 3의 경우 −0.4, 처리 2 - 처리 3의 경우 −0.2입니다.
각 처리의 효과는 해당 처리와 (해당 처리를 포함한) 모든 다른 처리 차이의 중위수의 평균입니다. 이 예의 데이터인 경우 효과(2) = [중위수 (2 – 1) + 중위수 (2 – 2) + 중위수 (2 – 3)]/3 = (0.00 + 0.00 – 0.20)/3 = −0.0667입니다. 마찬가지로 효과(1) = −0.1333이고 효과(3) = 0.20입니다.
수정된 블럭 중위수를 계산하려면 관측치에서 적절한 처리 효과를 빼서 각 관측치를 수정하십시오. 수정된 블럭 중위수는 각 블럭 내에서 계산된, 이렇게 수정된 데이터의 중위수입니다. 총 중위수는 수정된 블럭 중위수의 중위수입니다. 각 처리 수준에 대한 추정 중위수는 처리 효과에 총 중위수를 더한 값입니다.
- M. Hollander and D.A. Wolfe (1973). Nonparametric Statistical Methods, John Wiley & Sons, Inc., pp. 158 – 161.
같은 값 순위매기기
- 괸측치를 오름차순으로 정렬합니다.
- 같은 값이 없는 것처럼 각 관측치에 순위를 지정합니다.
- 같은 값의 집합인 경우, 해당하는 순위의 평균을 계산하여 이 값을 해당 집합에 있는 각 같은 값에 새 순위로 지정합니다.
예
표본에 2.4, 5.3, 2.4, 4.0, 1.2, 3.6, 4.0, 4.3, 4.0의 9개 관측치가 있습니다.
| 관측치 | 순위(같은 값이 없는 것으로 가정) | 순위 |
|---|---|---|
| 1.2 | 1 | 1 |
| 2.4 | 2 | 2.5 |
| 2.4 | 3 | 2.5 |
| 3.6 | 4 | 4 |
| 4.0 | 5 | 6 |
| 4.0 | 6 | 6 |
| 4.0 | 7 | 6 |
| 4.3 | 8 | 8 |
| 5.3 | 9 | 9 |
- 같은 값의 집합 수 = 2
- 첫 번째 집합의 같은 값 수 = 2
- 두 번째 집합의 같은 값 수 = 3
