원하는 방법 또는 공식을 선택하십시오.
이 항목의 내용
데이터 쌍들의 평균
데이터 쌍들의 평균(Walsh 평균이라고도 함)은 데이터 집합에 있는 값의 가능한 각 쌍(각 값을 자기 자신과 묶은 쌍도 포함)의 평균입니다.
공식
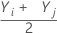= 모든 데이터 쌍들의 평균(i ≤ j)
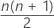= 데이터 쌍들의 평균의 총 수
표기법
| 용어 | 설명 |
|---|---|
| Yi | 데이터 집합에서 i번째 값 |
| Yj | 데이터 집합에서 j번째 값 |
| n | 표본 크기 |
추정 중위수
W( 1 )< W( 2 )< ... < W( M )을 데이터 쌍들의 평균(Walsh 평균이라고도 함) 순서가 있는 값으로 지정합니다. 여기서 M = n(n+1)/2입니다. M이 홀수이면 추정 중위수는 중간 값입니다. M이 짝수이면 추정 중위수는 두 중간 값의 평균입니다. Minitab에서는 Johnson and Mizoguchi (1978)1을 기반으로 하는 알고리즘을 사용하여 모집단 중위수의 점 추정치를 얻습니다.
- D.B. Johnson and T. Mizoguchi (1978). "Selecting the Kth Element in X + Y and X1 + X2 + ... + Xm," SIAM Journal of Computing 7, pp.147-153.
Wilcoxon 통계량
Wilcoxon 통계량은 귀무 가설에서의 중위수보다 큰 데이터 쌍들의 평균(Walsh 평균이라고도 함) 수에 귀무 가설에서의 중위수와 같은 데이터 쌍들의 평균 수의 1/2를 더한 값입니다. Wilcoxon 통계량은 W로 표시됩니다. Minitab에서는 Johnson and Miizoguchi (1978)1를 기반으로 하는 알고리즘을 사용하여 검정 통계량을 얻습니다.
- D.B. Johnson and T. Mizoguchi (1978). "Selecting the Kth Element in X + Y and X1 + X2 + ... + Xm," SIAM Journal of Computing 7, 147-153.
p-값
Wilcoxon 검정 통계량 W는 귀무 가설에서의 중위수를 초과하는 관측치와 연관된 순위의 합입니다. Minitab에서는 Johnson and Mizoguchi1에 설명된 대로 데이터 쌍들의 (Walsh) 평균을 사용하여 검정 통계량을 계산합니다.
- 관측치 수 N은 귀무 가설에서의 중위수와 같은 각 관측치에 대해 1씩 감소합니다. 그 결과 표본 크기는 n입니다.
- 귀무 가설에서의 중위수와 같은 관측치를 제외합니다. 관측치의 n(n + 1) / 2개의 데이터 쌍들의 Walsh 평균 (Yi + Yj) / 2(i ≤ j)를 계산합니다.
표본 크기가 큰 경우 W의 분포는 근사적으로 정규 분포를 따릅니다. 구체적으로 다음과 같습니다.
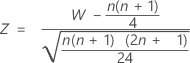는 근사적으로 평균이 0이고 표준 편차가 1인 정규 분포 N(0,1)를 따릅니다.
세 대립 가설의 정규 근사 p-값은 0.5의 연속성 수정을 사용합니다.
| 대립 가설 | p-값 |
|---|---|
| H1: 중위수 > 귀무 가설에서의 중위수 |  |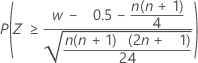
| H1: 중위수 < 귀무 가설에서의 중위수 |  |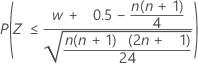
| H1: 중위수 ≠ 귀무 가설에서의 중위수 |  |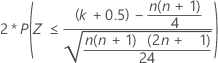
표기법
| 용어 | 설명 |
|---|---|
| n | 귀무 가설에서의 중위수 값과 같은 관측치를 제외한 후 관측된 데이터 점의 수 |
| W | Wilcoxon 검정 통계량 |
| w | 귀무 가설에서의 중위수를 초과하는 Walsh 평균의 수 + 귀무 가설에서의 중위수와 같은 Walsh 평균 수의 1/2. |
| k |  |
- D.B. Johnson and T. Mizoguchi (1978). "Selecting the Kth Element in X + Y and X1 + X2 + ... + Xm," SIAM Journal of Computing 7, pp.147-153.
신뢰 구간
신뢰 구간은 신뢰 수준(α = 1 - (percent confidence) / 100)을 사용하여 H0: 중위수 = d의 검정이 H1: 중위수 ≠ d에 대해 기각되지 않는 값(d)의 집합입니다. Wilcoxon 통계량이 이산형이기 때문에 1-표본 Wilcoxon 검정이 신뢰 구간을 달성하지 못하는 경우도 있습니다. 이 때문에 Minitab에서는 연속성 수정이 있는 정규 근사를 사용하여 달성 가능한 가장 가까운 신뢰 수준을 계산합니다.
