다음 방법 및 공식은 검정 평균과 기준 평균의 차이를 검정하는 데 사용됩니다.
차이, 표준 편차, 피실험자 내 표준 편차
차이
동등성 검정에 대한 차이 D는 다음과 같이 계산됩니다.
SE
차이에 대한 표준 오차는 다음과 같이 계산됩니다.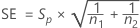
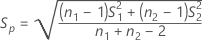
피실험자 내 표준 편차
피실험자 내 표준 편차 Sw는 다음과 같이 계산됩니다.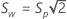
표기법
| 용어 | 설명 |
|---|---|
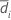 | 시퀀스 i의 표본 평균(자세한 내용은 2x2 교차 설계에 대한 동등성 검정에서 사용되는 공통적인 개념에 대한 방법 및 공식에서 확인하십시오.) |
| ni | 시퀀스 i의 피실험자 수 |
| Si | 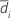 의 표본 표준 편차(시퀀스 i) 의 표본 표준 편차(시퀀스 i) |
신뢰 구간
100(1-α)% CI
기본적으로 Minitab에서는 다음 공식을 사용하여 동등성의 100(1 – α)% 신뢰 구간(CI)을 계산합니다.
CI = [min(C, Dl), max(C, Du)]
설명:

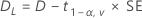
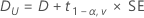
100(1-2α)% CI
100(1 – 2 α)% CI를 사용하는 옵션을 선택하는 경우 CI가 다음 공식에 의해 계산됩니다.
CI = [Dl, Du]
단측 구간
검정 평균 > 기준 평균 또는 검정 평균 - 기준 평균 > 하한 가설의 경우 100(1 – α)% 하한은 DL과 같습니다.
검정 평균 < 기준 평균 또는 검정 평균 - 기준 평균 < 상한 가설의 경우 100(1 – α)% 상한은 DU와 같습니다.표기법
| 용어 | 설명 |
|---|---|
| D | 검정 평균과 기준 평균의 차이 |
| SE | 표준 오차 |
| δ1 | 동등성 하한 |
| δ2 | 동등성 상한 |
| v | 자유도 |
| α | 검정의 유의 수준(알파) |
| t1-α, v | 자유도가 v인 t-분포의 1 - α 임계값 상한 |
t-값
t1을 가설  에 대한 t-값, t2를 가설
에 대한 t-값, t2를 가설  에 대한 t-값으로 정의합니다. 여기서
에 대한 t-값으로 정의합니다. 여기서  는 검정 모집단 평균과 기준 모집단 평균의 차이입니다. 기본적으로 t-값은 다음과 같이 계산됩니다.
는 검정 모집단 평균과 기준 모집단 평균의 차이입니다. 기본적으로 t-값은 다음과 같이 계산됩니다.


 에 대한 t-값, t2를 가설
에 대한 t-값, t2를 가설  에 대한 t-값으로 정의합니다. 여기서
에 대한 t-값으로 정의합니다. 여기서  는 검정 모집단 평균과 기준 모집단 평균의 차이입니다. 기본적으로 t-값은 다음과 같이 계산됩니다.
는 검정 모집단 평균과 기준 모집단 평균의 차이입니다. 기본적으로 t-값은 다음과 같이 계산됩니다.


검정 평균 > 기준 평균 가설의 경우 δ1 = 0입니다.
검정 평균 < 기준 평균 가설의 경우 δ 2 = 0입니다.
표기법
| 용어 | 설명 |
|---|---|
| D | 표본 검정 평균과 표본 기준 평균의 차이 |
| SE | 차이의 표준 오차 |
| δ1 | 동등성 하한 |
| δ2 | 동등성 상한 |
P-값
각 귀무 가설(H0)에 대한 확률 PH0은 다음과 같이 지정됩니다.
| H0 | P-값 |
|---|---|
 |
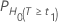 |
 |
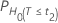 |
표기법
| 용어 | 설명 |
|---|---|
 | 검정 모집단 평균과 기준 모집단 평균의 알 수 없는 차이 |
| δ1 | 동등성 하한 |
| δ2 | 동등성 상한 |
| v | 자유도 |
| T | 자유도가 v인 t-분포 |
| t1 | 다음 가설에 대한 t-값:  |
| t2 | 다음 가설에 대한 t-값:  |
참고
t-값이 계산되는 방법에 대한 정보는 t-값에 대한 절을 참조하십시오.
