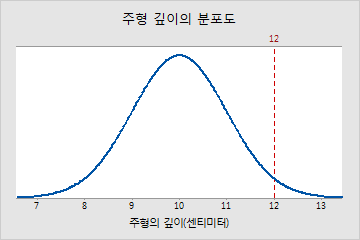
Z-값은 Z-검정에 대한 검정 통계량으로, 관측된 표본 통계량과 귀무 가설에서의 모집단 모수 간의 차이를 표준 편차 단위로 측정합니다. 예를 들어, 공업용 주형의 평균 깊이가 10cm이고 표준 편차가 1cm입니다. 깊이가 12cm인 주형은 평균보다 2 표준 편차만큼 크기 때문에 Z-값이 2입니다. 세로선이 이 관측치 및 전체 모집단으로부터의 상대적인 위치를 나타냅니다.
관측치를 Z-값으로 변환하는 것을 표준화라고 합니다. 모집단의 관측치를 표준화하려면 관측치에서 모집단 평균을 뺀 다음 그 결과를 모집단 표준 편차로 나눕니다. 이 계산으로 해당 관측치와 관련된 Z-값이 생성됩니다.
Z-값을 사용하여 귀무 가설의 기각 여부를 확인할 수 있습니다. 귀무 가설의 기각 여부를 확인하려면 Z-값을 대부분의 통계 문헌에서 찾을 수 있는 임계값과 비교하십시오. 임계값은 양측 검정의 경우 Z1-α/2, 단측 검정의 경우 Z1-α입니다. Z-값의 절대값이 임계값보다 큰 경우 귀무 가설을 기각합니다. 그렇지 않으면 귀무 가설을 기각할 수 없습니다.
예를 들어, 두 번째 주형 그룹의 평균 깊이가 10cm인지 여부를 확인하려고 합니다. 두 번째 그룹에 속한 각 주형의 깊이를 측정한 다음 그룹의 평균 깊이를 계산합니다. 1-표본 Z-검정에서 −1.03의 Z-값을 계산합니다. 0.05의 α를 선택하면 임계값이 1.96이 됩니다. Z-값의 절대값이 1.96보다 작기 때문에 귀무 가설을 기각할 수 없으며 주형의 평균 깊이가 10cm와 다르다는 결론을 내릴 수 없습니다.
