자유도는 알 수 없는 모집단 모수의 값을 추정하고 이러한 추정치의 변동성을 계산하는 데 "사용"할 수 있는 데이터가 제공하는 정보 양입니다. 이 값은 표본의 관측치 수와 모형의 모수 수에 따라 결정됩니다.
표본 크기를 증가시키면 모집단에 대한 더 많은 정보가 제공되므로, 데이터의 자유도가 증가합니다. 모형에 모수를 추가하면(예를 들어, 회귀 방정식에서 항 수를 증가시켜) 데이터의 정보를 "사용"하게 되어 모수 추정치의 변동성을 추정하는 데 사용할 수 있는 자유도가 감소됩니다.
또한 자유도는 특정 분포를 특성화하는 데 사용됩니다. t, F 및 카이-제곱 등 여러 분포에서 자유도를 사용하여 다양한 표본 크기 및 모형 모수 수에 적합한 t, F 또는 카이-제곱 분포를 지정할 수 있습니다. 예를 들어, 다음 표에서는 자유도가 서로 다른 카이-제곱 분포 간의 차이를 설명합니다.
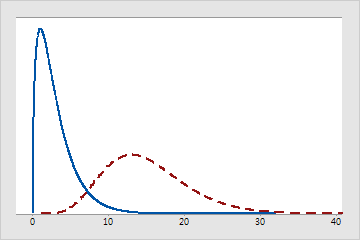
자유도가 다른 카이-제곱 분포
실선 분포의 자유도는 3입니다. 파선 분포의 자유도는 15입니다.
예제
예를 들어, 1-표본 t-검정은 유일한 모수인 모평균을 추정합니다. 표본 크기 n은 모집단 평균과 이 평균의 변동성을 추정하기 위한 n개 정보를 구성합니다. 자유도 하나는 평균을 추정하는 데 사용되고, 나머지 n-1개의 자유도는 변동성을 추정합니다. 따라서 1-표본 t-검정은 자유도가 n-1인 t-분포를 사용합니다.
반대로, 다중 선형 회귀 분석의 경우 모형에 포함할 항마다 모수 하나를 추정해야 하며, 자유도 하나를 사용합니다. 따라서 다중 선형 회귀 모형에 너무 많은 항을 포함하면 모수의 변동성을 추정하는 데 사용할 수 있는 자유도가 감소하고 모형의 신뢰도가 떨어질 수 있습니다.
