Anderson-Darling 통계량

Anderson-Darling 통계량은 데이터가 특정 분포를 얼마나 잘 따르는지 측정합니다. 지정된 데이터 집합 및 분포의 경우, 분포가 데이터에 더 적합할수록 이 통계량의 값은 더 작아집니다. 예를 들어, Anderson-Darling 통계량을 사용하여 데이터가 t-검정의 정규성 가정을 충족하는지 확인할 수 있습니다.

선택한 분포에서 데이터를 추출하는 경우 해당하는 p-값을 사용하여(사용 가능한 경우) 검정할 수 있습니다. p-값이 선택된 알파(보통 0.05 또는 0.10)보다 작으면 데이터가 해당 분포를 따른다는 귀무 가설을 기각합니다. Anderson-Darling 검정의 p-값은 수학적으로 존재하지 않는 경우도 있기 때문에 Minitab에서 항상 Anderson-Darling 검정의 p-값을 표시하지는 않습니다.

또한 Anderson-Darling 통계량을 사용하면 여러 분포를 비교하여 적합도가 가장 높은 분포를 찾아낼 수 있습니다. 그러나 어떤 분포가 가장 적합하다는 결론을 내리려면 해당 분포의 Anderson-Darling 통계량이 다른 분포의 통계량보다 상당히 작아야 합니다. 통계량이 서로 가까운 경우에는 확률도 등 추가 기준을 사용하여 여러 분포 중에서 선택해야 합니다.

분포	Anderson-Darling	p-값
지수 분포	9.599	p < 0.003
정상 체중	0.641	p < 0.089
3-모수 Weibull 분포	0.376	p < 0.432

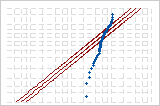
지수 분포

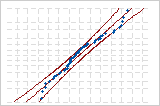
정상 체중

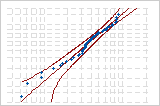
3-모수 Weibull 분포

Minitab에서는 (선택한 분포를 기반으로 하고 최대우도 추정 방법 또는 최소 제곱 추정치를 사용한) 확률도의 적합선과 비모수 단계 함수 간의 가중 제곱 거리를 사용하여 Anderson-Darling 통계량을 계산합니다. 분포의 꼬리에서는 더 많은 가중치가 부여됩니다.