특정 모집단 특성(예: 평균)에 대한 정보를 확인하려는 경우, 일반적으로 전체 모집단을 측정하는 것이 불가능하기 때문에 해당 모집단에서 랜덤 표본을 추출합니다. 이 표본을 사용하여 해당하는 표본 특성을 계산하며, 이 표본 특성이 알 수 없는 모집단 특성에 대한 정보를 요약하는 데 사용됩니다. 관심의 대상이 되는 모집단 특성을 모수라고 하며 해당하는 표본 특성을 표본 통계량 또는 모수 추정치라고 합니다. 통계량은 표본에서 얻은 모수에 대한 정보의 요약이므로 통계량의 값은 모집단에서 추출한 특정 표본에 따라 달라집니다. 그 값은 표본에 따라 랜덤하게 변하므로, 통계량은 랜덤 양(변수)입니다. 이 랜덤 변수의 확률 분포를 표본 추출 분포라고 합니다. (표본) 통계량의 표본 추출 분포는 랜덤 표본을 기준으로 해당하는 모집단 모수에 대한 결론을 내릴 수 있기 때문에 중요합니다.
예를 들어, 정규 분포를 따르는 모집단에서 랜덤 표본을 추출하는 경우 표본 평균이 하나의 통계량입니다. 현재 표본을 기반으로 한 표본 평균의 값이 모평균의 추정치입니다. 이 추정치는 동일한 정규 모집단에서 다른 표본을 추출하는 경우 랜덤하게 달라집니다. 이러한 변화를 설명하는 확률 분포가 표본 평균의 표본 추출 분포입니다. 통계량의 표본 추출 분포는 가능한 모든 통계량 값 및 특정 범위의 통계량 값이 발생하는 빈도를 지정합니다. 상위 모집단이 정규 분포를 따르는 경우 표본 평균의 표본 추출 분포도 정규 분포를 따릅니다.
다음 절에서 모수, 모수 추정치 및 표본 추출 분포에 대한 추가 정보를 제공합니다.
모수
모수는 분포 곡선을 생성하기 위해 확률 분포 함수(PDF)의 입력 값으로 사용되는 모집단 전체를 설명하는 측도입니다. 표본 통계량과 구분하기 위해 모수는 대부분 그리스 문자로 나타냅니다. 예를 들어, 모평균은 그리스 문자 뮤(μ)로 나타내며 모집단 표준 편차는 그리스 문자 시그마(σ)로 나타냅니다. 모수는 고정된 상수로 변수처럼 변하지 않습니다. 그러나 전체 모집단을 측정하는 것은 불가능하기 때문에 일반적으로 해당 값은 알 수 없습니다.
| 분포 | 모수 1 | 모수 2 | 모수 3 |
|---|---|---|---|
| 카이-제곱 분포 | 자유도 | ||
| 정규 분포 | 평균 | 표준 편차 | |
| 3-모수 감마 분포 | 형상 | 척도 | 분계점 |
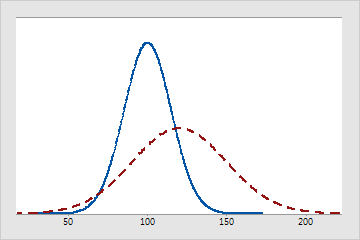
실선은 평균이 100이고 표준 편차가 15인 정규 분포를 나타냅니다. 파선도 정규 분포이지만, 평균이 120이고 표준 편차가 30입니다.
모수 추정치(표본 통계량이라고도 함)
모수는 전체 모집단의 기술 측정값입니다. 그러나 전체 모집단을 측정하는 것은 불가능하기 때문에 일반적으로 해당 값은 알 수 없습니다. 이런 이유로 모집단에서 랜덤 표본을 추출하여 모수 추정치를 구할 수 있습니다. 통계 분석의 목적 중 하나는 이 추정치와 관련된 오차의 양과 함께 모집단 모수의 추정치를 얻기 위한 것입니다. 이 추정치를 표본 통계량이라고도 합니다.
- 점 추정치는 모수의 가장 비슷한 단일 값입니다. 예를 들어, 모집단 평균(모수)의 점 추정치는 표본 평균(모수 추정치)입니다.
- 신뢰 구간은 모집단 모수를 포함할 가능성이 있는 값의 범위입니다.
예를 들어, 점화 플러그 제조업체에서 점화 플러그 간격의 문제를 조사하고 있다고 가정합니다. 제조되는 모든 점화 플러그를 측정하는 데는 너무 많은 비용이 듭니다. 대신, 100개의 점화 플러그를 랜덤하게 추출하여 간격(밀리미터)을 측정합니다. 표본의 평균은 9.2입니다. 이 값은 모평균(μ)의 점 추정치입니다. μ에 대한 95% 신뢰 구간(8.8, 9.6)도 만듭니다. 즉, 모든 점화 플러그에 대한 평균 간격의 참 값이 8.8과 9.6 사이에 있다고 95% 확신할 수 있습니다.
표본 추출 분포
| 호박 | 1 | 2 | 3 | 4 | 5 | 6 |
| 무게 | 19 | 14 | 15 | 12 | 16 | 17 |
전체 모집단을 알고 있지만, 예를 들기 위해 모집단에서 3개의 호박이 포함되는 가능한 모든 랜덤 표본을 추출합니다(랜덤 표본 20개). 그런 다음 각 표본의 평균을 계산합니다. 표본 평균의 표본 추출 분포는 3개의 호박을 포함하는 가능한 모든 랜덤 표본에 대한 모든 표본 평균으로 설명되며, 다음 표에 표시되어 있습니다.
| 표본 | 무게 | 평균 무게 | 확률 |
|---|---|---|---|
| 2, 3, 4 | 14, 15, 12 | 13.7 | 1/20 |
| 2, 4, 5 | 14, 12, 16 | 14 | 1/20 |
| 2, 4, 6 | 14, 12, 17 | 14.3 | 2/20 |
| 3, 4, 5 | 15, 12, 16 | ||
| 3, 4, 6 | 15, 12, 17 | 14.7 | 1/20 |
| 1, 2, 4 | 19, 14, 12 | 15 | 3/20 |
| 2, 3, 5 | 14, 15, 16 | ||
| 4, 5, 6 | 12, 16, 17 | ||
| 2, 3, 6 | 14, 15, 17 | 15.3 | 2/20 |
| 1, 3, 4 | 19, 15, 12 | ||
| 1, 4, 5 | 19, 12, 16 | 15.7 | 2/20 |
| 2, 5, 6 | 14, 16, 17 | ||
| 1, 2, 3 | 19, 14, 15 | 16 | 3/20 |
| 3, 5, 6 | 15, 16, 17 | ||
| 1, 4, 6 | 19, 12, 17 | ||
| 1, 2, 5 | 19, 14, 16 | 16.3 | 1/20 |
| 1, 2, 6 | 19, 14, 17 | 16.7 | 2/20 |
| 1, 3, 5 | 19, 15, 16 | ||
| 1, 3, 6 | 19, 15, 17 | 17 | 1/20 |
| 1, 5, 6 | 19, 16, 17 | 17.3 | 1/20 |
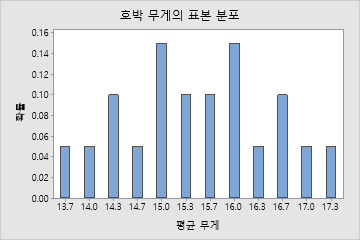
실제로는 위의 예와 같이 표본 추출 분포를 표로 작성할 수 없습니다. 표본의 상위 모집단을 알고 있는 최상의 경우라 하더라도 관심의 대상이 되는 표본 통계량의 정확한 표본 추출 분포를 알 수 없습니다. 그러나 표본 통계량의 표본 추출 분포를 근사할 수 있는 경우도 있습니다. 예를 들어, 정규 모집단에서 표본을 추출하면 표본 평균이 정확히 정규 분포를 따릅니다.
그러나 정규 모집단이 아닌 모집단에서 표본을 추출하는 경우 표본 평균의 정확한 분포를 알 수 없을 수도 있습니다. 그러나 중심 극한 정리에 따라 표본이 충분히 크면 표본 평균이 대략적으로 정규 분포를 따릅니다. 따라서 모집단을 알 수 없지만 표본이 충분히 크면 예를 들어 모집단 평균의 특정 표준 편차 숫자 내에 표본 평균이 있을 확률은 85%라고 말할 수 있습니다.
