왜도
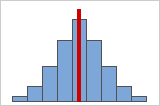
그림 A
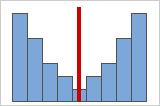
그림 B
대칭 분포 또는 치우치지 않은 분포
데이터가 대칭에 가까울수록 왜도 값이 0에 근접합니다. 그림 A는 정의에 따르면 비교적 왜도를 거의 나타내지 않는 정규 분포 데이터를 보여줍니다. 정규 데이터의 이 히스토그램 가운데에서 아래로 선을 그리면 양면이 서로 거울에 비친 이미지임을 쉽게 알 수 있습니다. 그러나 왜도 부족만으로 정규성을 의미하지는 않습니다. 그림 B는 분포의 양면이 여전히 서로 거울에 비추는 이미지이지만 데이터는 정규 분포에서 멀리 떨어져 있는 분포를 보여줍니다.
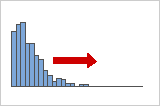
양수 또는 왼쪽으로 치우친 분포
분포의 "꼬리"가 오른쪽을 가리키고 해당 왜도 값이 0보다 크거나 양수이기 때문에 양수로 기울거나 왼쪽으로 치우친 데이터의 이름이 지정됩니다. 월급 데이터의 경우 회사의 많은 사원이 비교적 적은 월급을 받지만 점점 더 적은 사람만 매우 많은 월급을 받는 식으로 자주 치우칩니다.
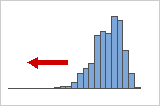
음수 또는 왼쪽으로 치우친 분포
분포의 "꼬리"가 왼쪽을 가리키고 왜도 값이 음수이기 때문에 왼쪽으로 치우치거나 음수로 기운 데이터로 지정됩니다. 고장율 데이터는 대부분 왼쪽으로 치우칩니다. 너무 적은 수의 전구만 바로 꺼지고 대다수는 오랫동안 켜져 있습니다.
첨도
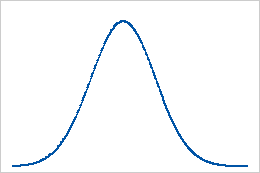
기준선: 0의 첨도 값
완전히 정규 분포를 따르는 데이터의 첨도 값은 0입니다 정규 분포를 따르는 데이터가 첨도의 기준선을 설정합니다. 표본 첨도가 0으로부터 유의하게 벗어나면 데이터가 정규 분포를 따르지 않는다는 것을 나타냅니다.
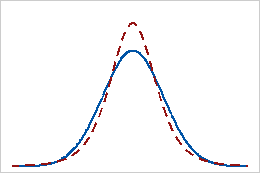
양의 첨도
분포의 첨도 값이 양수이면 분포의 꼬리가 정규 분포보다 두껍다는 것을 나타냅니다. 예를 들어, t 분포를 따르는 데이터의 첨도 값은 양수입니다. 실선은 정규 분포, 점선은 첨도 값이 양수인 분포를 보여줍니다.
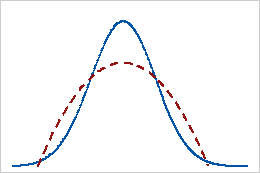
음의 첨도
분포의 첨도 값이 음수이면 분포의 꼬리가 정규 분포보다 얇다는 것을 나타냅니다. 예를 들어, 첫 번째와 두 번째 형상 모수가 2인 베타 분포를 따르는 데이터의 첨도 값은 음수입니다. 실선은 정규 분포, 점선은 첨도 값이 음수인 분포를 보여줍니다.
