중심 극한 정리는 확률 및 통계의 기초 정리입니다. 이 정리는 분산이 유한한 모집단에서 추출한 랜덤 표본의 평균 분포를 설명합니다. 표본 크기가 충분히 크면 평균의 분포가 근사적으로 정규 분포를 따릅니다. 이 정리는 모집단 분포의 모양에 관계없이 적용됩니다. 많은 통계 절차에는 정규 데이터가 필요합니다. 중심 극한 정리를 사용하면 상당히 비정규적인 모집단에도 이와 같이 유용한 절차를 적용할 수 있습니다. 필요한 표본 크기는 원래 분포의 모양에 따라 달라집니다. 모집단의 분포가 대칭인 경우 표본 크기가 5면 적절합니다. 모집단의 분포가 극히 비대칭인 경우에는 표본 크기가 50 이상으로 더 커야 합니다. 예를 들어, 표본 크기가 50보다 크면 평균의 분포가 근사적으로 정규 분포를 따를 수도 있습니다. 다음 그래프는 분포가 필수 표본 크기에 미치는 영향의 예를 보여줍니다.
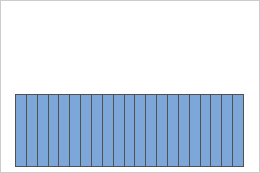
균등 분포
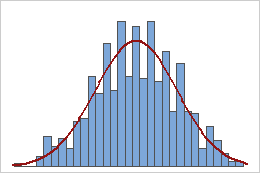
표본 평균
균등 모집단의 표본
균등 분포를 따르는 모집단은 대칭이지만 첫 번째 히스토그램에서 보듯이 매우 비정규적입니다. 그러나 이 모집단에서 선택한 크기가 5인 1,000개 표본 평균의 분포는 중심 극한 정리에 따라 두 번째 히스토그램에서 보듯이 거의 정규 분포를 따릅니다. 표본 평균의 이 히스토그램에는 정규성을 나타내기 위해 추가된 정규 곡선이 포함됩니다.
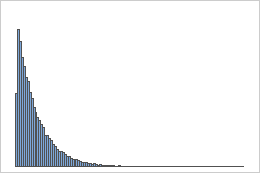
지수 분포
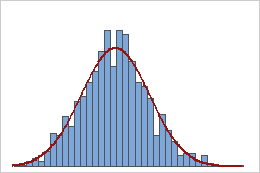
표본 평균
지수 모집단의 표본
지수 분포를 따르는 모집단은 첫 번째 히스토그램에서 보듯이 비대칭이고 비정규적입니다. 그러나 이 모집단에서 선택한 크기가 50인 1,000개 표본 평균의 분포는 중심 극한 정리에 따라 두 번째 히스토그램에서 보듯이 거의 정규 분포를 따릅니다. 표본 평균의 이 히스토그램에는 정규성을 나타내기 위해 추가된 정규 곡선이 포함됩니다.
