임계값은 귀무 가설 하 검정 통계량의 분포에서 귀무 가설을 기각해야 하는 값의 집합을 정의하는 점입니다. 이 집합은 임계 또는 기각 영역이라고 합니다. 일반적으로, 단측 검정에는 하나의 임계값이 있고 양측 검정에는 두 개의 임계값이 있습니다. 임계값은 귀무 가설이 참일 때 검정 통계량 값이 검정의 기각 영역에 포함될 확률이 유의 수준(α 또는 알파로 표시됨)과 같도록 결정됩니다.
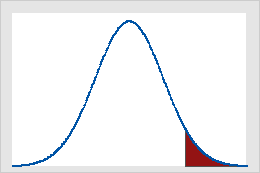
그림 A
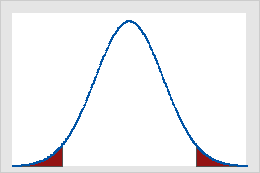
그림 B
α = 0.05인 경우 표준 정규 분포의 임계값
그림 A는 검정 통계량의 값이 임계값 1.64보다 크거나 같으면 단측 Z 검정의 결과가 유의하다는 것을 보여줍니다. 다른 색상으로 표시된 부분이 곡선 아래 넓이의 제1종 오류 확률(이 예의 경우 α = 5%)을 나타냅니다. 이 경우 그림 B는 검정 통계량의 절대값이 임계값 1.96보다 크거나 같으면 양측 Z 검정의 결과가 유의하다는 것을 보여줍니다. 다른 색상으로 표시된 두 부분의 합이 곡선 아래 넓이의 5%(α)를 차지합니다.
임계값 계산의 예
가설 검정에서 표본에 H0를 기각하거나 H0를 기각하지 못하기에 충분한 증거가 있는지 확인하는 데는 두 가지 방법이 있습니다. 가장 일반적인 방법은 p-값을 사전 지정된 α 값과 비교하는 것입니다(α는 H0가 참일 때 H0를 기각할 확률입니다). 하지만, 이와 동일한 한 가지 방법은 데이터에 기반한 검정 통계량의 값을 임계값과 비교하는 것입니다. 다음은 1-표본 t-검정 및 일원 분산 분석의 임계값을 계산하는 방법입니다.
1-표본 t-검정을 위한 임계값 계산
- 을 선택합니다.
- 역 누적 확률을 선택합니다.
- 자유도에 9(관측치 수 - 1)를 입력합니다.
- 입력 상수에 0.95(1 - 1/2 알파)를 입력합니다.
이렇게 하면 임계값과 같은 역 누적확률 1.83311을 얻게 됩니다. t-통계량의 절대값이 이 임계값보다 크면 0.10의 유의 수준에서 귀무 가설, H0를 기각할 수 있습니다. t-통계량의 절대값이 이 임계값보다 크면 0.10의 유의 수준에서 귀무 가설, H0를 기각할 수 있습니다.
분산 분석을 위한 임계값 계산
- 을 선택합니다.
- 역 누적 확률을 선택합니다.
- 분자 자유도에 2(요인 수준 수 - 1)를 입력합니다.
- 분모 자유도에 9(오차에 대한 자유도)를 입력합니다.
- 입력 상수에 0.95(1 - 알파)를 입력합니다.
이렇게 하면 역 누적 확률(임계값) 4.25649를 얻게 됩니다. F-통계량이 이 임계값보다 크면 0.05의 유의 수준에서 귀무 가설 H0를 기각할 수 있습니다.
