신뢰 구간은 표본 통계량에서 파생되어 알 수 없는 모집단 모수 값이 포함될 가능성이 있는 값의 범위입니다. 표본은 랜덤하게 추출하는 특성이 있기 때문에 특정 모집단에서 선택한 두 표본의 신뢰 구간이 동일하게 될 가능성은 없습니다. 그러나 표본 추출을 여러 번 반복하면 일정한 백분율의 신뢰 구간에는 알 수 없는 모집단 모수가 포함됩니다.
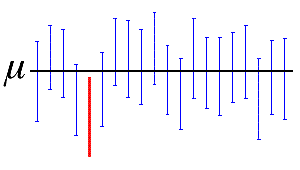
여기서 검은색 수평선은 알 수 없는 모평균 µ의 고정 값을 나타냅니다. 수평선과 겹치는 파란색 수직 신뢰 구간에는 모평균의 값이 포함됩니다. 완전히 수평선 아래 있는 빨간색 신뢰 구간에는 모평균의 값이 포함되지 않습니다. 95% 신뢰 구간은 한 모집단에서 선택한 20개의 표본 중 19개(95%)가 모집단 모수를 포함하는 신뢰 구간을 생성할 것임을 나타냅니다.
신뢰 구간을 사용하여 모집단 모수의 추정치를 평가할 수 있습니다. 예를 들어, 제조업체에서는 생산하는 연필의 평균 길이가 목표 길이와 다른지 알고 싶어합니다. 제조업체에서는 연필의 랜덤 표본을 추출하여 표본의 평균 길이가 52mm이고 95% 신뢰 구간이 (50,54)임을 확인합니다. 따라서 모든 연필의 평균 길이가 50mm와 54mm 사이에 있다고 95% 확신할 수 있습니다.
- 점 추정치
- 이 단일 값은 표본 데이터를 사용하여 모집단 모수를 추정합니다.
- 오차 한계
-
통계량을 사용하여 값을 추정하는 경우, 연구가 얼마나 적절하게 설계되었든지 관계 없이 추정치에는 랜덤 표본 추출 오차가 있습니다. 오차 한계는 이 오차를 수량화하며 추정치의 정밀도를 나타냅니다.
아마도 오차 한계가 설문조사 결과와 관계가 있다고 이미 알고 있습니다. 예를 들어 정당 여론 조사의 결과 후보의 승인 등급이 55%이며 오차 한계는 5%라고 보고됩니다. 즉, 실제 승인 등급은 +/- 5%를 고려하여 50%와 60% 사이라는 의미입니다.
양측 신뢰 구간의 경우 오차 한계는 추정 통계량에서 각 신뢰 구간 값까지의 거리입니다. 신뢰 구간이 대칭인 경우, 오차 한계는 신뢰 구간의 너비의 반입니다. 예를 들어 캠축의 평균 추정 길이가 600mm이고 신뢰 구간의 범위가 599에서 601까지인 경우, 오차 한계는 1입니다. 오차 한계는 1입니다.
오차 한계가 클수록 구간이 넓고, 점 추정치의 값에 대해 더 확신할 수 없게 됩니다.
