두 변수 사이의 관계를 평가하는 경우 변수들이 어떻게 관련되어 있는지 파악하는 것이 중요합니다. 선형 관계가 가장 일반적이지만 변수들이 아래 표시된 것과 같이 비선형 또는 단조 관계를 가지고 있는 경우도 있습니다. 변수 사이에 관계가 없을 수도 있습니다. 관계를 평가하려면 먼저 변수의 산점도를 작성해야 합니다.
선형 관계는 직선으로 모형화할 수 있는 데이터의 추세입니다. 예를 들어, 한 항공사에서 연료 가격이 운항 비용에 미치는 영향을 추정하려고 합니다. 여객기 연료 1갤런의 가격이 1달러 오르면, 로스앤젤레스와 뉴욕 간의 운항 비용이 약 3,500달러 정도 증가합니다. 즉, 여객기 연료 가격과 운항 비용 사이에 선형 관계가 있음을 나타냅니다.
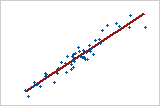
그림 1: 강한 양의 선형 관계
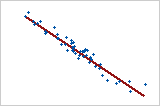
그림 2: 강한 음의 선형 관계
두 변수가 동시에 일정한 비율로 증가하거나 감소하는 경우 양의 선형 관계가 존재합니다. 그림 1에서는 점들이 선 가까이에 붙어 있는데, 이것은 변수들의 관계가 강한 것을 나타냅니다. 이 관계의 Pearson 상관 계수는 +0.921입니다.
한 변수가 감소할 때 다른 변수는 증가하는 경우 음의 상관 관계가 존재합니다. 그림 2에서는 점들이 선 가까이에 붙어 있는데, 이것은 변수들의 관계가 강한 것을 나타냅니다. 이 관계의 Pearson 상관 계수는 -0.968입니다.
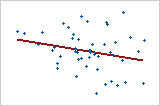
그림 3: 약한 선형 관계
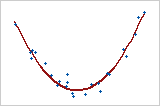
그림 4: 비선형 관계
그림 3의 데이터 점들은 랜덤하게 분포되어 있는 것으로 보입니다. 점들은 선에 가까이 붙어 있지 않은데, 이것은 관계가 존재하더라도 매우 약한 관계라는 것을 나타냅니다. 이 관계의 Pearson 상관 계수는 -0.253입니다.
두 변수 사이의 관계가 선형이 아닌 경우 한 변수가 변하면 증가 또는 감소 비율이 달라지며, 데이터에 "곡선 패턴"이 발생합니다. 이러한 곡선 추세는 2차 또는 3차 함수 등 비선형 함수를 사용하여 더 잘 모형화할 수 있으며, 선형으로 변환할 수도 있습니다. 그림 4는 두 변수 사이의 강한 관계를 보여줍니다. 그러나 관계가 선형이 아니기 때문에 Pearson 상관 계수는 +0.244에 불과합니다. 이 그림은 관계를 파악하기 위해 데이터를 그래프로 표시하는 것이 중요하다는 것을 보여줍니다.
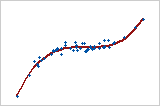
그림 5: 단조 관계
단순 관계에서 두 변수는 동일한 상대적인 방향으로 이동하는 경향이 있지만 반드시 일정한 비율로 변화하는 것은 아닙니다. 선형 관계에서 두 변수는 동일한 방향으로 일정한 비율로 이동합니다. 그림 5는 두 변수가 동시에 증가하지만 같은 비율로 증가하지는 않음을 보여줍니다. 이 관계는 단조 관계이며 선형이 아닙니다. 이 데이터의 Pearson 상관 계수는 0.843이지만 Spearman 상관 계수는 더 높습니다(0.948).
선형 관계는 단조 관계이기도 합니다. 예를 들어, 그림 1에 표시된 관계는 단조 및 선형 관계입니다.
