검정을 지정하고 유의 수준을 지정하며 대립 가설을 선택합니다.
이 항목의 내용
특이치 검정
Minitab의 모든 특이치 검정은 표본의 단일 특이치를 탐지할 수 있습니다. 일반적으로 Grubbs의 검정이 잘 작동합니다. 그러나 표본에 가능한 특이치가 두 개 이상 포함되어 있는 경우 Grubbs의 검정과 Dixon의 Q 비율이 효과적이지 못할 수도 있습니다.
데이터에 대해 두 개 이상의 특이치 검정을 수행하지 마십시오. 특이치 검정을 수행하고 검정에서 식별된 특이치를 제거한 다음 두 번째 특이치 검정을 수행하면 실제로 특이치가 아닌 값을 제거할 위험이 있습니다. 이 위험을 피하려면 상황에 가장 적합한 유형의 특이치 검정을 선택하십시오.
- 데이터에 특이치가 포함되어 있는지 여부를 알 수 없으면 Grubbs의 검정을 사용하십시오.
- 데이터에 하나 이상의 특이치가 포함되어 있으면 Dixon의 검정 중 하나를 사용하십시오. Dixon의 검정은 여러 개의 잠재적인 특이치가 일으킬 수 있는 마스크 효과를 해결할 수 있습니다.
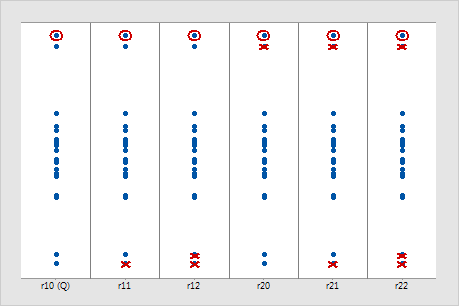
다음 그림에서 각 열은 여러 Dixon의 비율 검정에서 동일한 표본을 처리하는 방법을 보여줍니다. 원으로 표시된 값이 잠재적인 특이치입니다. X는 각 Dixon의 비율 검정에서 검정 통계량을 계산할 때 무시하는 데이터 값을 나타냅니다. (이 그림에서는 대립 가설이 가장 작거나 가장 큰 데이터 값이 특이치 또는 가장 큰 데이터 값이 특이치라고 가정합니다.) 이 데이터에 대해서는 Dixon의 r22 비율 검정이 원으로 표시된 값을 특이치로 식별할 가능성이 가장 높습니다.
정규 모집단에서 큰 표본을 추출할수록 극단값이 포함될 가능성이 높습니다. Dixon은 비율에 대한 다음과 같은 일반 지침을 제안했습니다.
| 표본 크기(n) | 권장되는 비율 |
|---|---|
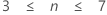 |
r10(Dixon의 Q 비율이라고도 함) |
 |
r11 |
 |
r21 |
 |
r22 |
유의 수준
귀무 가설(H0)을 기각할지 여부를 결정하려면 유의 수준을 p-값과 비교하십시오. p-값이 유의 수준보다 작은 경우, 일반적으로 결과가 통계적으로 유의하다고 해석하고 H0을 기각합니다.
일반적으로 0.05의 유의 수준(α 또는 알파로 표시함)이 적절합니다. 0.05의 유의 수준은 실제로 차이가 없는데 차이가 존재한다는 결론을 내릴 위험이 5%라는 것을 나타냅니다.
- 존재할 가능성이 있는 차이를 더 확실히 탐지하려면 더 높은 유의 수준(예: 0.10)을 선택하십시오. 예를 들어, 한 품질 엔지니어가 새 볼 베어링의 안정성을 현재 베어링의 안정성과 비교합니다. 불안정한 볼 베어링이 심각한 문제를 일으킬 수 있기 때문에 엔지니어는 새 볼 베어링이 안정적이라는 것을 확인해야 합니다. 엔지니어는 볼 베어링 안정성의 가능한 차이를 더 확실히 탐지하기 위해 0.10의 유의 수준을 선택합니다.
- 실제로 존재하는 차이만 더 확실히 탐지하려면 더 낮은 유의 수준(예: 0.01)을 선택하십시오. 예를 들어, 한 제약 회사의 과학자는 회사의 새 약품이 증상을 유의하게 완화시킨다는 주장이 참이라는 것을 확인해야 합니다. 과학자는 증상에 유의한 차이가 존재하지 않는다는 것을 더 확실히 확인하기 위해 0.001의 유의 수준을 선택합니다.
무엇을 결정하시겠습니까?(대립 가설)
무엇을 결정하시겠습니까?(대립 가설)에서 다음 대립 가설 검정 중 하나를 선택합니다.
- 가장 작거나 가장 큰 데이터 값이 특이치: 가장 작은 데이터 값 또는 가장 큰 데이터 값이 특이치일 수 있는 경우 이 양측 검정을 사용합니다. 이 양측 검정은 가장 작거나 가장 큰 데이터 값에 대한 특이치를 탐지할 수 있지만 단측 검정보다 검정력이 낮습니다.
- 가장 작은 데이터 값이 특이치: 가장 작은 데이터 값이 특이치인지 의심스러운 경우 이 단측 검정을 사용합니다. 이 단측 검정은 양측 검정보다 검정력이 크지만 가장 큰 데이터 값인 특이치를 탐지할 수 없습니다.
- 가장 큰 데이터 값이 특이치: 가장 큰 데이터 값이 특이치인지 의심스러운 경우 이 단측 검정을 사용합니다. 이 단측 검정은 양측 검정보다 검정력이 크지만 가장 작은 데이터 값인 특이치를 탐지할 수 없습니다.
