Dixon의 검정 통계량
- i는 의심스러운 특이치 데이터 쪽(위쪽 또는 아래쪽)에 있는 극단값의 수를 나타냅니다. i = 1 또는 2입니다.
- j는 데이터의 반대쪽에 있는 극단값의 수를 나타냅니다. j = 0, 1, 2입니다.
예를 들어, 의심스러운 특이치가 표본의 가장 작은 값이지만 비상정적으로 큰 값 두 개도 표본에 포함되어 있는 경우 r12가 적절한 검정 통계량입니다. r10(Dixon의 Q라고도 함)은 표본에 하나의 극단값만 포함되어 있는 경우 적절한 검정 통계량입니다.
Dixon의 검정 통계량에 대한 임계값은 Rorabacher(1991)에 표로 정리되어 있습니다.
단측 검정 통계량


양측 검정 통계량

표기법
| 용어 | 설명 |
|---|---|
| rij | Dixon의 검정 통계량(i = 1, 2; j = 0, 1, 2) |
| yi | 표본에서 i번째로 작은 값 |
| n | 표본의 관측치 수 |
참고 문헌
- D.B. Rorabacher (1991). "Statistical Treatment for Rejection of Deviant Values: Critical Values of Dixon Q Parameter and Related Subrange Ratios at the 95 percent Confidence Level," Analytic Chemistry, 83, 2, 139-146.
- E.P. King (1953). "On Some Procedures for the Rejection of Suspected Data," Journal of the American Statistical Association, Vol. 48, No. 263, 531-533.
Grubbs의 검정 통계량
단측 통계량을 위한 공식

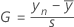
양측 통계량을 위한 공식
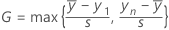
표기법
| 용어 | 설명 |
|---|---|
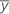 | 표본 평균 |
| yi | 표본에서 i번째로 작은 값 |
| s | 표본의 표준 편차 |
| n | 표본의 관측치 수 |
Dixon 검정 통계량의 p-값

검정 통계량에 대한 누적분포함수
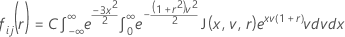

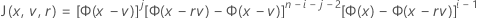
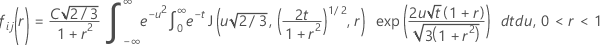
Minitab에서는 30-점 Gauss-Laguerre 구적법을 사용하여 내부 적분을 평가합니다. Minitab에서는 30점 Gauss-Hermite 구적법을 사용하여 외부 적분을 평가합니다.
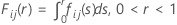
McBane(2006)과 유사하게 Minitab에서는 16-점 Gauss-Legendre 구적법을 사용하여 Fij(r)를 계산합니다.
단측 검정의 p-값

단측 검정의 p-값

또한 King의 관측 결과 위의 근사는 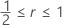 에 대해 동일하게 됩니다.
에 대해 동일하게 됩니다.
표기법
| 용어 | 설명 |
|---|---|
| rij | Dixon 검정 통계량(i = 1, 2; j = 0, 1, 2) |
| yi | 표본에서 i번째로 작은 값 |
| n | 표본의 관측치 수 |
참고 문헌
W.J. Dixon (1951). "Ratios Involving Extreme Values," Annals of Mathematical Statistics, 22(1), 68-78.
E.P. King (1953). "On Some Procedures for the Rejection of Suspected Data," Journal of the American Statistical Association, Vol. 48, No. 263, pages 531-533.
G.C. McBane (2006). "Programs to Compute Distribution Functions and Critical Values for Extreme Value Ratios for Outlier Detection," Journal of Statistical Software, Vol. 16, No. 3, pages 1-9.
Grubbs 검정 통계량의 p-값
단측 검정을 위한 공식

양측 검정을 위한 공식

정확한 p-값 대 근사 p-값

그렇지 않은 경우에는 계산된 p-값이 정확한 p-값에 대한 상한을 나타냅니다. 그러나 상한은 정확한 p-값의 매우 좋은 근사값입니다.
표기법
| 용어 | 설명 |
|---|---|
| G | Grubbs의 검정 통계량 |
| n | 표본의 관측치 수 |
| T | 자유도가 n – 2인 t-분포를 따르는 랜덤 변수 |
