특이치 검정을 해석하려면 다음 단계를 수행하십시오. 주요 결과에는 p-값, 특이치 및 특이치 그림이 포함됩니다.
1단계: 특이치의 존재 여부 확인
특이치가 존재하는지 여부를 확인하려면 p-값을 유의 수준과 비교하십시오. 일반적으로 0.05의 유의 수준(α 또는 알파로 표시함)이 적절합니다. 0.05의 유의 수준은 실제로 특이치가 존재하지 않는데 특이치가 존재한다는 결론을 내릴 위험이 5%라는 것을 나타냅니다.
- p-값 ≤ α: 특이치가 존재함(H0 기각)
- p-값이 유의 수준보다 작거나 같으면 귀무 가설을 기각하고 특이치가 존재한다는 결론을 내립니다. 특이치의 원인을 식별해 보십시오. 모든 데이터 입력 오류 또는 측정 오류를 수정하십시오. 비정상적인 일회성 사건과 연관된 데이터 값을 삭제해 보십시오(특수 원인).
- p-값 > α: 특이치가 존재한다는 결론을 내릴 수 없음(H0 기각 실패)
- p-값이 유의 수준보다 크면 특이치가 존재한다는 결론을 내릴 충분한 증거가 없기 때문에 귀무 가설을 기각할 수 없습니다. 검정에 특이치를 탐지하기에 충분한 검정력이 있는지 확인해야 합니다. 자세한 내용은 검정력 증대에서 확인하십시오.
방법
| 귀무 가설 | 모든 데이터 값이 동일한 정규 모집단에서 추출됩니다. |
|---|---|
| 대립 가설 | 가장 작은 데이터 값이 특이치 |
| 유의 수준 | α = 0.05 |
Grubbs의 검정
| 변수 | N | 평균 | 표준 편차 | 최소값 | 최대값 | G | P |
|---|---|---|---|---|---|---|---|
| 파괴강도 | 14 | 123.4 | 46.3 | 12.4 | 193.1 | 2.40 | 0.044 |
특이치
| 변수 | 행 | 특이치 |
|---|---|---|
| 파괴강도 | 10 | 12.38 |
주요 결과: P
이 결과에서 귀무 가설은 모든 데이터 값이 동일한 정규 모집단에서 추출되었다는 것입니다. p-값이 0.044로, 유의 수준 0.05보다 작기 때문에 귀무 가설을 기각하고 특이치가 존재한다는 결론을 내립니다.
2단계: 특이치의 값 확인
검정에서 데이터의 특이치를 식별하면 Minitab에서 특이치 표를 표시합니다. 특이치의 값 및 특이치가 포함된 워크시트의 행을 확인하려면 특이치 표를 사용하십시오.
방법
| 귀무 가설 | 모든 데이터 값이 동일한 정규 모집단에서 추출됩니다. |
|---|---|
| 대립 가설 | 가장 작은 데이터 값이 특이치 |
| 유의 수준 | α = 0.05 |
Grubbs의 검정
| 변수 | N | 평균 | 표준 편차 | 최소값 | 최대값 | G | P |
|---|---|---|---|---|---|---|---|
| 파괴강도 | 14 | 123.4 | 46.3 | 12.4 | 193.1 | 2.40 | 0.044 |
특이치
| 변수 | 행 | 특이치 |
|---|---|---|
| 파괴강도 | 10 | 12.38 |
주요 결과: 행, 특이치
이 결과에서 특이치의 값은 12.38이고 10행에 있습니다.
3단계: 특이치를 시각적으로 식별
데이터의 특이치를 식별하려면 특이치 그림을 사용합니다. 특이치가 존재하면 Minitab에서는 그림에서 빨간색 정사각형으로 표시합니다. 특이치의 원인을 식별합니다. 모든 데이터 입력 오류 또는 측정 오류를 수정합니다. 비정상적인 일회성 사건에 대한 데이터 값을 삭제합니다(특수 원인이라고도 함).
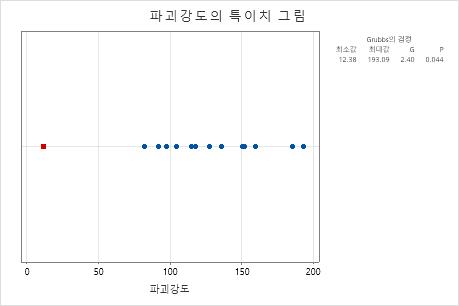
이 특이치 그림에서 가장 작은 값인 12.38은 특이치입니다.
