한 나무 손잡이 회사의 품질 엔지니어가 빗자루 손잡이의 랜덤 표본에 대한 강도를 검사합니다. 엔지니어는 각 손잡이를 부러뜨리는 데 필요한 힘을 기록합니다. 엔지니어는 데이터 그래프를 생성하며 표본의 값 중 하나가 비정상적으로 작다는 것을 알았습니다.
엔지니어는 최소값이 특이치인지 여부를 확인하기 위해 특이치 검정을 수행합니다.
- 표본 데이터 핸들강도.MWX를 엽니다.
- 을 선택합니다.
- 변수에 파괴강도을 입력합니다.
- 옵션을 클릭합니다.
- 무엇을 결정하시겠습니까?(대립 가설)에서 가장 작은 데이터 값이 특이치을 선택합니다.
- 각 대화 상자에서 확인을 클릭합니다.
결과 해석
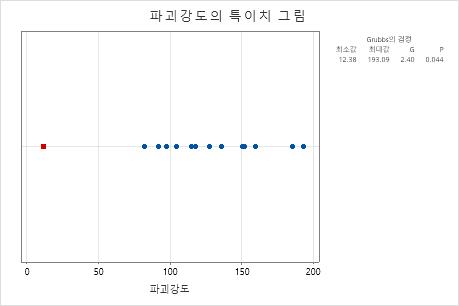
표본의 평균은 123.4입니다. G 통계량은 가장 작은 값 12.38이 평균보다 2.4 표준 편차가 작다는 것을 나타냅니다. p-값은 모든 값이 실제로 동일한 정규 분포 모집단에서 추출된 경우 이렇게 작은 최소값을 얻을 확률이 0.044에 지나지 않는다는 것을 나타냅니다. p-값이 0.044로, 유의 수준(α 또는 알파로 표시됨) 0.05보다 작기 때문에 엔지니어는 귀무 가설을 기각하고 가장 작은 값이 특이치라는 결론을 내립니다.
엔지니어는 조사 결과 데이터를 입력한 사람이 123.8 대신 12.38로 잘못 입력했다는 것을 발견했습니다.
방법
| 귀무 가설 | 모든 데이터 값이 동일한 정규 모집단에서 추출됩니다. |
|---|---|
| 대립 가설 | 가장 작은 데이터 값이 특이치 |
| 유의 수준 | α = 0.05 |
Grubbs의 검정
| 변수 | N | 평균 | 표준 편차 | 최소값 | 최대값 | G | P |
|---|---|---|---|---|---|---|---|
| 파괴강도 | 14 | 123.4 | 46.3 | 12.4 | 193.1 | 2.40 | 0.044 |
특이치
| 변수 | 행 | 특이치 |
|---|---|---|
| 파괴강도 | 10 | 12.38 |