평균
평균은 데이터 중심을 나타내는 하나의 값으로 표본을 설명합니다. 평균은 모든 관측치의 합을 관측치 수로 나눈, 데이터의 평균으로 계산됩니다.
N
표본 크기(N)는 표본의 총 관측치 수입니다.
해석
표본 크기는 검정의 검정력에 영향을 미칩니다.
일반적으로 표본 크기가 클수록 검정에서 표본 데이터와 정규 분포 간의 차이를 탐지할 검정력이 높습니다. 즉, 실제로 차이가 존재할 때 표본 크기가 클수록 차이를 탐지할 확률이 높아집니다.
표준 편차
표준 편차는 산포, 즉 데이터가 평균을 중심으로 퍼져 있는 정도를 나타내는 가장 일반적인 측도입니다. 표본 표준 편차가 클수록 데이터가 평균 주위로 더 넓게 퍼져 있다는 것을 나타냅니다.
AD
Anderson-Darling 적합도 통계량(AD)은 적합선(정규 분포에 근거)과 경험적 분포 함수(데이터 점에 근거) 사이의 영역을 측정합니다. Anderson-Darling 통계량은 분포의 끝 부분에 더 많은 가중치를 부여한 거리 제곱입니다.
해석
Minitab에서는 Anderson-Darling 통계량을 사용하여 p-값을 계산합니다. p-값은 귀무 가설에 반하는 증거를 측정하는 확률입니다. p-값이 작을수록 귀무 가설에 반하는 더 강력한 증거가 됩니다. Anderson-Darling 통계량 값이 크면 데이터가 정규 분포를 따르지 않는다는 것을 나타냅니다.
KS
Kolmogorov-Smirnov 검정은 표본 데이터의 ECDF(경험적 누적분포함수)와 데이터가 정규일 경우 예상되는 분포를 비교합니다.
해석
Minitab에서는 Kolmogorov-Smirnov 통계량을 사용하여 p-값을 계산합니다. p-값은 데이터가 정규 분포를 따르는 경우 최소한 표본에서 계산된 값만큼 극단적인 검정 통계량(예: Kolmogorov-Smirnov 통계량)을 얻을 확률입니다. Kolmogorov-Smirnov 통계량 값이 더 크면 데이터가 정규 분포를 따르지 않는다는 것을 나타냅니다.
RJ
Ryan-Joiner 통계량은 데이터와 데이터의 정규 점수 사이의 상관을 계산하여 데이터가 정규 분포를 얼마나 잘 따르는지 측정합니다. 상관 계수가 1에 가까우면 모집단이 정규 분포를 따를 가능성이 높습니다. 이 검정은 Shapiro-Wilk 정규성 검정과 비슷합니다.
해석
Minitab에서는 Ryan-Joiner 통계량을 사용하여 p-값을 계산합니다. p-값은 데이터가 정규 분포를 따르는 경우 최소한 표본에서 계산된 값만큼 극단적인 검정 통계량(예: Ryan-Joiner 통계량)을 얻을 확률입니다. Ryan-Joiner 통계량 값이 더 크면 데이터가 정규 분포를 따르지 않는다는 것을 나타냅니다.
p-값
p-값은 귀무 가설에 반하는 증거를 측정하는 확률입니다. p-값이 작을수록 귀무 가설에 반하는 더 강력한 증거가 됩니다.
해석
데이터가 정규 분포를 따르지 않는지 여부를 확인하려면 p-값을 사용하십시오.
- p-값 ≤ α: 데이터가 정규 분포를 따르지 않음(H0 기각)
- p-값이 유의 수준보다 작거나 같으면 귀무 가설을 기각하고 데이터가 정규 분포를 따르지 않는다는 결론을 내립니다.
- p-값 > α: 데이터가 정규 분포를 따르지 않는다는 결론을 내릴 수 없음(H0 기각 실패)
- p-값이 유의 수준보다 크면 귀무 가설을 기각할 수 없습니다. 데이터가 정규 분포를 따르지 않는다는 결론을 내릴 충분한 증거가 없습니다.
확률도
확률도는 추정 누적 확률을 기준으로 각 관측치의 값을 표시하여 표본으로부터 추정 누적분포함수(CDF)를 만듭니다.
해석
정규 분포가 데이터에 얼마나 적합한지 시각화하려면 확률도를 사용합니다.
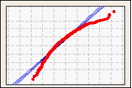
오른쪽으로 치우친 데이터
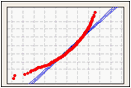
왼쪽으로 치우친 데이터
팁
Minitab에서 백분위수와 값의 차트를 보려면 적합된 분포선 위로 마우스를 가져가십시오.
