이 항목의 내용
Anderson-Darling 통계량(A2)
A2는 적합선(선택된 분포에 근거)과 비모수적 계단 함수(표시 점에 근거) 사이의 영역을 측정합니다. 이 통계량은 분포의 끝 부분에 더 많은 가중치를 부여한 거리 제곱입니다. Anderson-Darling 값이 작을수록 분포가 데이터를 보다 잘 적합시킵니다..
Anderson-Darling 정규성 검정은 다음과 같이 정의됩니다.
H0: 데이터가 정규 분포를 따름
H1: 데이터가 정규 분포를 따르지 않음
공식

표기법
| 용어 | 설명 |
|---|---|
| F(Yi) |  , 표준 정규 분포의 누적 분포 함수 , 표준 정규 분포의 누적 분포 함수 |
| Yi | 순서가 있는 데이터 |
Anderson-Darling 정규성 검정에 대한 p-값
Anderson-Darling 정규성 검정의 결과를 보고하기 위한 한 가지 양적 측도는 p-값입니다. 작은 p-값은 귀무 가설이 거짓임을 나타냅니다.
A 2를 알면 p-값을 계산할 수 있습니다.
다음과 같이 설정합니다.
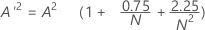
- 13 > A'2 > 0.60인 경우 p = exp(1.2937 - 5.709 * A'2 + 0.0186(A'2)2)
- 0.60 > A'2 > 0.34인 경우 p = exp(0.9177 - 4.279 * A'2 – 1.38(A'2)2)
- 0.34 > A'2 > 0.20인 경우 p = 1 – exp(–8.318 + 42.796 * A'2 – 59.938(A'2)2)
- A'2 < 0.200인 경우 p = 1 – exp(–13.436 + 101.14 * A'2 – 223.73(A'2)2)
비결측값 개수(N)
표본에 있는 비결측값의 개수입니다.
표준 편차
표본 표준 편차는 데이터 산포의 측도를 제공하며, 표본 분산의 제곱근과 같습니다.
공식
 이면 표본의 표준 편차는 다음과 같습니다.
이면 표본의 표준 편차는 다음과 같습니다.
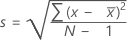
표기법
| 용어 | 설명 |
|---|---|
| x i | i번째 관측치 |
 | 관측치의 평균 |
| N | 비결측 관측치 수 |
분산
분산은 데이터가 평균 주위에 분산된 정도를 측정합니다. 분산은 표준 편차의 제곱과 같습니다.
공식
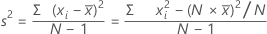
표기법
| 용어 | 설명 |
|---|---|
| xi | i번째 관측치 |
 | 관측치의 평균 |
| N | 비결측 관측치 수 |
왜도
왜도는 비대칭성을 나타내는 척도입니다. 음수 값은 왼쪽 왜도를 나타내고 양수 값은 오른쪽 왜도를 나타냅니다. 0 값이 반드시 대칭성을 나타내지는 않습니다.
공식
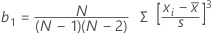
표기법
| 용어 | 설명 |
|---|---|
| xi | i번째 관측치 |
 | 관측치의 평균 |
| N | 비결측 관측치 수 |
| s | 표본의 표준 편차 |
첨도
첨도는 분포가 정규 분포와 어떻게 다른지 나타내는 측도입니다. 양수 값은 일반적으로 분포의 정점이 정규 분포보다 뾰족하다는 것을 나타냅니다. 음수 값은 분포의 정점이 정규 분포보다 납작하다는 것을 나타냅니다.
공식

표기법
| 용어 | 설명 |
|---|---|
| xi | i번째 관측치 |
 | 관측치의 평균 |
| N | 비결측 관측치 수 |
| s | 표본의 표준 편차 |
평균
숫자 묶음의 중심을 측정하는 데 가장 일반적으로 사용되는 측도. 모든 관측치의 합을 (비결측) 관측치 수로 나눈 값입니다.
공식
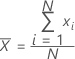
표기법
| 용어 | 설명 |
|---|---|
| xi | i번째 관측치 |
| N | 비결측 관측치 수 |
최소값
데이터 집합에서 가장 작은 값입니다.
최대값
데이터 집합에서 가장 큰 값입니다.
제1 사분위수(Q1)
표본 관측치의 25%가 제1 사분위수 값보다 작거나 같습니다. 따라서 제1st 사분위수를 25번째 백분위수라고도 합니다.
공식

표기법
| 용어 | 설명 |
|---|---|
| y | w의 절사된 정수 값 |
| w | 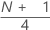 |
| z | w의 절사된 부분 성분 |
| xj | 가장 작은 값에서 가장 큰 값 순으로 정렬된 표본 데이터 리스트의 j번째 관측치 |
참고
w가 정수인 경우 y = w, z = 0 및 Q1 = xy입니다.
중위수
표본 중위수는 데이터의 중간에 있습니다. 절반 이상의 관측치가 표본 중위수보다 작거나 같고 절반 이상의 관측치는 표본 중위수보다 크거나 같습니다.
값이 N개 포함된 열이 있다고 가정합니다. 중위수를 계산하려면 먼저 데이터를 가장 작은 값에서 가장 큰 값 순으로 정렬하십시오. N이 홀수이면 표본 중위수는 중간에 있는 값입니다. N이 짝수이면 표본 중위수는 중간에 있는 두 값의 평균입니다.
예를 들어, N = 5이고 데이터 x1, x2, x3, x4, x5가 있는 경우 중위수 = x3입니다.
N = 6이고 순서가 있는 데이터 x1, x2, x3, x4, x5, x6이 있는 경우:

여기서 x3과 x4는 세 번째와 네 번째 관측치입니다.
제3 사분위수(Q3)
표본 관측치의 75%가 제3 사분위수 값보다 작거나 같습니다. 따라서 제3 사분위수를 75번째 백분위수라고도 합니다.
공식

표기법
| 용어 | 설명 |
|---|---|
| y | w의 절사된 값 |
| w |
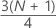 |
| z | w의 절사된 부분 성분 |
| xj | 가장 작은 값에서 가장 큰 값 순으로 정렬된 표본 데이터 리스트의 j번째 관측치 |
참고
w가 정수인 경우 y = w, z = 0 및 Q3 = xy입니다.
평균에 대한 신뢰 구간
공식

표기법
| 용어 | 설명 |
|---|---|
 | 평균 |
| s | 표본의 표준 편차 |
| N | 비결측값 수 |
| t N, α | 1 – α / 2에서 자유도가 N - 1인 t 분포의 역 누적 확률, α = 1 – 신뢰 수준 / 100 |
중위수에 대한 신뢰 구간
Minitab에서는 비선형 보간법을 사용하여 실제 중위수에 대한 신뢰 구간을 계산합니다. 1. 이 방법은 정규 분포, Cauchy 분포, 균등 분포 등 다양한 대칭 분포에 아주 좋은 근사입니다. 비대칭 분포의 예는 항상 선형 보간법보다 훨씬 더 정확한 적절한 결과를 보여줍니다.
표준 편차에 대한 신뢰 구간
Minitab에서는 모집단 표준 편차 σ에 대한 (1 – α) 100% 신뢰 구간을 계산합니다. 신뢰 구간은 데이터가 정규 분포를 따른다는 가정에 매우 민감합니다. 정규성을 조금만 벗어나도 신뢰 구간이 잘못될 수 있습니다.
공식
신뢰 구간은 다음과 같이 계산됩니다.
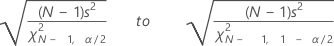
표기법
| 용어 | 설명 |
|---|---|
| s | 표준 편차 |
| N | 비결측값 수 |
| χ2N, α | 1 – α / 2에서 자유도가 N인 χ2의 역 누적 확률, α = 1 – 신뢰 수준 / 100 |
