추정 평균
공식
포아송 분포의 평균은 다음과 같이 추정됩니다.
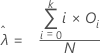
계산
| 데이터 | 2 2 3 3 2 4 4 2 1 1 1 4 4 3 0 4 3 2 3 3 4 1 3 1 4 3 2 2 1 2 0 2 3 2 3 |
| 범주(i) | 관측(Oi) | 추정 평균 | 포아송 확률(pi) |
|---|---|---|---|
| 0 | 2 | 0 * 2 = 0 | p0 = e-2.4 = 0.090718 |
| 1 | 6 | 1 * 6 = 6 | p1 = e-2.4 * 2.4 = 0.217723 |
| 2 | 10 | 2 * 10 = 20 | p2 = e-2.4 * (2.4)2/ 2! = 0.261268 |
| 3 | 10 | 3 * 10 = 30 | p3 = e-2.4 * (2.4)3/ 3! = 0.209014 |
 |
7 | 4 * 7 = 28 | p4 = 1 - (p0 + p1 +p2 + p3) = 0.221267 |
N = 35
Σ (i * Oi) = 84
추정 평균 = 
표기법
| 용어 | 설명 |
|---|---|
| N | 모든 관측치의 합(O0 + O1 + ...+ Ok) |
| k | (범주 수) - 1 |
| Oi | i번째 범주에서 관측된 사건 수 |
| pi | 포아송 확률 |
범주 수
Minitab에서는 다음과 같은 반복적인 방법을 사용하여 범주를 결정합니다.
첫 번째 범주 정의
pi = P(X 
xi )로 설정합니다.
i = 1로 설정합니다. N*pi 
2인 경우 첫 번째 범주는 "
x 1"로 정의됩니다. N*pi < 2인 경우 i를 1 증가시키고 반복합니다. N*p 2 
2인 경우 첫 번째 범주는 "
x 2"로 정의됩니다. N*pi < 2인 경우 i를 1 증가시키고 N*pi 
2일 때까지 반복합니다. 이 조건이 처음으로 충족되거나 xi가 세 번째로 큰 데이터 값일 때 반복을 중단하고 첫 번째 범주를 "
xi "로 정의합니다. 첫 번째 범주의 값이 0인 경우 첫 번째 범주는 "<" 또는 "=" 부호 없이 "0"으로 정의됩니다. 첫 번째 범주와 연관된 확률과 기대값은 각각 pi 및 N*pi입니다. 첫 번째 범주에 대한 관측치는 
xi인 모든 데이터 값의 개수입니다.
마지막 범주 정의
개념적으로 마지막 범주를 정의하는 것은 첫 번째 범주를 정의하는 것과 비슷하지만, Minitab에서는 가장 큰 데이터 값부터 시작하여 반대로 정의합니다.
마지막 범주는 "
xj "이며, 여기서 xj는 범주의 기대값이 2보다 큰 (1 + 첫 번째 범주의 데이터 값)보다 큰 가장 큰 데이터 값입니다. 마지막 범주에 대한 확률과 기대값은 각각 pj 및 N*pj이고, 관측치는 
xj인 데이터 값의 개수입니다.
중간 범주 정의
첫 번째와 마지막 범주를 정의한 후 Minitab에서는 첫 번째와 마지막 범주 사이의 범주를 결정합니다. "X 
k"를 첫 번째 범주, "X 
m"을 마지막 범주로 설정합니다. (k, m) 사이 모든 정수의 기대값이 
2인 경우 모두 중간 범주를 구성합니다. 그렇지 않은 경우 Minitab에서는 반복 루프를 사용하여 여러 개의 인접한 정수를 기대값 
2인 범주로 분류합니다. 관측치 수가 적은 데이터 집합과 같이 범주의 기대값이 2보다 작은 경우도 있습니다.
표기법
| 용어 | 설명 |
|---|---|
| N | 총 관측치 수 |
| xi | 가장 작은 값에서 가장 큰 값의 순서로 정렬한 후 데이터 집합의 i번째 값 |
| pi | 포아송 확률 |
포아송 확률
공식
i번째 범주(i < k)의 포아송 확률:
마지막 범주에 대한 포아송 확률: i = k,
pi = 1 – (p0 + p1 + ...+ pk-1)
표기법
| 용어 | 설명 |
|---|---|
| k | 범주 수 |
| λ | 표본의 추정 평균 |
기대 개수
공식
i번째 범주의 기대 관측치 수는 N * pi입니다.
표기법
| 용어 | 설명 |
|---|---|
| N | 표본 크기 |
| pi | i번째 범주와 연관된 포아송 확률 |
카이-제곱에 대한 기여도
공식
I번째 범주의 카이-제곱 값에 대한 기여도는 다음과 같이 계산됩니다.
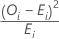
표기법
| 용어 | 설명 |
|---|---|
| OI | I번째 범주에서 관측된 관측치 수 |
| EI | I번째 범주의 기대 관측치 수 |
검정 통계량
공식
카이-제곱 적합도 검정 통계량은 다음과 같이 계산됩니다.
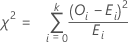
표기법
| 용어 | 설명 |
|---|---|
| k | (범주 수) - 1 |
| Oi | i번째 범주에서 관측된 관측치 수 |
| Ei | i번째 범주의 기대 관측치 수 |
p-값 및 자유도
p-값:
확률(X > 검정 통계량)
여기서 X는 MEAN 하위 명령을 사용하는 경우 자유도가 k - 1, MEAN 하위 명령을 사용하지 않는 경우 자유도가 k - 2인 카이-제곱 분포를 따릅니다.
계산
| 데이터 | 2 2 3 3 2 4 4 2 1 1 1 4 4 3 0 4 3 2 3 3 4 1 3 1 4 3 2 2 1 2 0 2 3 2 3 |
| 범주(i) | 관측(Oi) | 추정 평균 | 포아송 확률(pi) |
|---|---|---|---|
| 0 | 2 | 0 * 2 = 0 | p0 = e -2.4 = 0.090718 |
| 1 | 6 | 1 * 6 = 6 | p1 = e -2.4 * 2.4 = 0.217723 |
| 2 | 10 | 2 * 10 = 20 | p2 = e -2.4 * (2.4)2/ 2! = 0.261268 |
| 3 | 10 | 3 * 10 = 30 | p3 = e -2.4 * (2.4)3/ 3! = 0.209014 |
 |
7 | 4 * 7 = 28 | p4 = 1 - (p0 + p1 +p2 + p3 ) = 0.221267 |
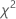= ( 0.43492 + 0.344527 + 0.080058 + 0.985114 + 0.071545) = 1.91622
k = 5= 범주 수
DF = 5- 2 = 3
p-값 = P (X > 1.91622) = 0.590
표기법
| 용어 | 설명 |
|---|---|
| k | 범주 수 |
| Oi | i번째 범주에서 관측된 관측치 수. |
| Ei | i번째 범주의 기대 관측치 수. |
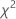 | 카이-제곱 적합도 검정 통계량 |
| DF | 자유도 |
