1단계: 데이터의 크기 설명
표본의 관측치 수를 확인하려면 N을 사용합니다. Minitab에서는 이 카운트에 결측값을 포함하지 않습니다.
중간에서 큰 데이터 표본을 수집해야 합니다. 관측치가 20개 미만인 표본은 보통 데이터의 분포를 적절하게 나타냅니다. 그러나 히스토그램을 사용하여 분포를 더 잘 나타내기 위해 일부 실무자는 관측치를 50개 이상 추출할 것을 권장합니다. 또한 표본이 클수록 공정 모수(예: 평균, 표준 편차)의 더 정확한 추정치를 제공합니다.
통계량
| 변수 | N | N* | 평균 | 평균의 표준 오차 | 표준 편차 | 최소값 | Q1 | 중위수 | Q3 | 최대값 |
|---|---|---|---|---|---|---|---|---|---|---|
| 회전력 | 68 | 0 | 21.2647 | 0.778784 | 6.42202 | 10 | 16 | 20 | 24.75 | 37 |
주요 결과: N
이 결과에는 관측치가 68개 있습니다.
2단계: 데이터의 중심 설명
데이터 중심을 나타내는 하나의 값으로 표본을 설명하려면 평균을 사용하십시오. 많은 통계 분석에서 평균을 데이터의 분포 중심에 대한 표준 측도로 사용합니다.
중위수는 데이터의 분포 중심에 대한 또 하나의 측도입니다. 중위수는 일반적으로 평균보다 특이치의 영향을 덜 받습니다. 데이터 값의 반은 중위수 값보다 크고, 데이터 값의 반은 중위수 값보다 작습니다.
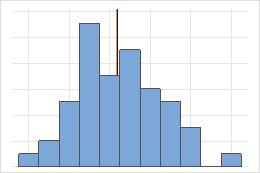
대칭
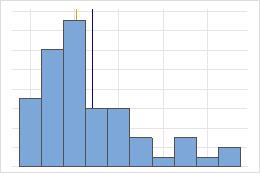
비대칭
대칭 분포의 경우 평균(파란색 선)과 중위수(주황색 선)가 너무 비슷하여 두 선을 모두 쉽게 볼 수 없습니다. 그러나 비대칭 분포는 오른쪽으로 치우칩니다.
통계량
| 변수 | N | N* | 평균 | 평균의 표준 오차 | 표준 편차 | 최소값 | Q1 | 중위수 | Q3 | 최대값 |
|---|---|---|---|---|---|---|---|---|---|---|
| 회전력 | 68 | 0 | 21.2647 | 0.778784 | 6.42202 | 10 | 16 | 20 | 24.75 | 37 |
주요 결과: 평균 및 중위수
이 결과에서 치약 뚜껑을 열기 위해 필요한 평균 회전력은 21.265이고 회전력의 중위수는 20입니다. 데이터는 오른쪽으로 치우쳐 있는 것으로 보이며, 이는 평균이 중위수보다 큰 이유를 설명합니다.
3단계: 데이터의 산포 설명
데이터가 평균을 중심으로 퍼져 있는 정도를 확인하려면 표준 편차를 사용합니다. 표준 편차 값이 클수록 데이터가 더 퍼져 있다는 것을 나타냅니다.
통계량
| 변수 | N | N* | 평균 | 평균의 표준 오차 | 표준 편차 | 최소값 | Q1 | 중위수 | Q3 | 최대값 |
|---|---|---|---|---|---|---|---|---|---|---|
| 회전력 | 68 | 0 | 21.2647 | 0.778784 | 6.42202 | 10 | 16 | 20 | 24.75 | 37 |
주요 결과: 표준 편차
이 결과에서 표준 편차는 6.422입니다. 정규 데이터의 경우, 대부분의 관측치는 평균의 양쪽으로 각각 3 표준 편차 내에 포함됩니다.
4단계: 데이터 분포의 모양과 산포 평가
데이터의 모양과 산포를 평가하고 잠재적 특이치를 식별하려면 히스토그램, 개별 값 그림 및 상자 그림을 사용하십시오.
데이터가 치우쳐 있는 것으로 보이는지 여부를 확인하려면 데이터의 산포를 조사합니다.
데이터가 치우쳐 있으면 대부분의 데이터가 그래프의 높은 쪽이나 낮은 쪽에 위치합니다. 일반적으로 히스토그램이나 상자 그림에서 왜도를 탐지하기가 가장 쉽습니다.
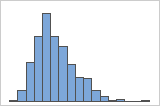
오른쪽으로 치우침
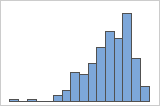
왼쪽으로 치우침
오른쪽으로 치우친 데이터의 히스토그램은 대기 시간을 보여줍니다. 대부분의 대기 시간이 비교적 짧고 몇 개의 대기 시간만 깁니다. 왼쪽으로 치우친 데이터의 히스토그램은 수명 데이터를 보여줍니다. 몇 개의 품목이 즉시 고장나고 더 많은 품목이 나중에 고장납니다.
데이터의 변동 정도 확인
표본의 변동성을 확인하려면 점들의 산포를 평가합니다. 표본의 변동성이 클수록 점들이 데이터의 중심에서 더 많이 분산됩니다.

이 개별 값 그림은 오른쪽 데이터의 변동이 왼쪽 데이터의 변동보다 더 크다는 것을 보여줍니다.
다봉 데이터 찾기
다봉 데이터에는 봉우리(최빈값이라고도 함)가 여러 개 있습니다. 다봉 데이터는 보통 중요한 변수가 아직 확인되지 않았다는 것을 의미합니다.
관측치를 그룹으로 분류할 수 있는 추가 정보가 있는 경우 이 정보를 사용하여 그룹 변수를 만들 수 있습니다. 그런 다음, 그룹으로 그래프를 생성하여 그룹 변수가 데이터의 봉우리를 설명하는지 여부를 확인할 수 있습니다.
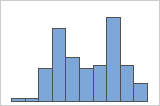
단순
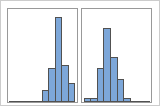
그룹 표시
예를 들어, 한 은행의 관리자가 대기 시간 데이터를 수집하여 단순 히스토그램을 생성합니다. 히스토그램에는 두 개의 봉우리가 있는 것으로 보입니다. 추가 조사 후, 관리자는 수표를 현금으로 바꾸려는 고객의 대기 시간이 부동산 융자를 신청하는 고객의 대기 시간보다 짧은 것을 확인합니다. 관리자는 고객 작업에 대한 그룹 변수를 추가한 후 그룹을 사용하여 히스토그램을 생성합니다.
특이치 식별
다른 데이터 값에서 멀리 떨어져 있는 데이터 값인 특이치는 분석 결과에 크게 영향을 미칠 수 있습니다. 일반적으로 상자 그림에서 특이치를 식별하기가 가장 쉽습니다.
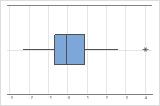
상자 그림에서는 별표(*)가 특이치를 나타냅니다.
특이치의 원인을 식별합니다. 모든 데이터 입력 오류 또는 측정 오류를 수정합니다. 비정상적인 일회성 사건에 대한 데이터 값을 삭제합니다(특수 원인이라고도 함). 그런 다음 분석을 반복합니다. 자세한 내용은 특이치 식별에서 확인하십시오.
5단계: 여러 그룹의 데이터 비교
데이터에 그룹을 나타내는 기준 변수가 있는 경우 기준 변수를 사용하여 그룹 또는 그룹 수준별로 데이터를 분석할 수 있습니다.
통계량
| 변수 | 기계 | N | N* | 평균 | 평균의 표준 오차 | 표준 편차 | 최소값 | Q1 | 중위수 | Q3 | 최대값 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 회전력 | 1 | 36 | 0 | 18.6667 | 0.732467 | 4.39480 | 10 | 15.25 | 17 | 21.75 | 30 |
| 2 | 32 | 0 | 24.1875 | 1.25839 | 7.11852 | 14 | 17.5 | 24 | 31 | 37 |
이 결과에서 요약 통계량은 기계별로 별도 계산됩니다. 각 기계에 대한 데이터의 중심과 산포의 차이를 쉽게 확인할 수 있습니다. 예를 들어, 기계 1의 평균 회전력과 변동이 기계 2보다 작습니다 평균의 차이가 유의한지 여부를 확인하기 위해 2-표본 t-검정을 수행할 수 있습니다.
