이 항목의 내용
상자 그림
상자 그림은 표본 분포의 그래픽 요약을 제공합니다. 상자 그림은 데이터의 모양, 중심 위치 및 변동성을 보여줍니다.
해석
데이터의 산포를 평가하고 잠재적 특이치를 식별하려면 상자 그림을 사용합니다. 상자 그림은 표본 크기가 20보다 클 때 가장 적합합니다.
- 치우친 데이터
-
데이터가 치우쳐 있는 것으로 보이는지 여부를 확인하려면 데이터의 산포를 조사합니다. 데이터가 치우쳐 있으면 대부분의 데이터가 그래프의 높은 쪽이나 낮은 쪽에 위치합니다. 일반적으로 히스토그램이나 상자 그림에서 왜도를 탐지하기가 가장 쉽습니다.
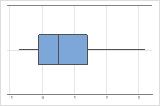
오른쪽으로 치우침
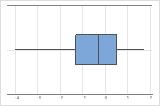
왼쪽으로 치우침
오른쪽으로 치우친 데이터의 상자 그림은 대기 시간을 보여줍니다. 대부분의 대기 시간이 비교적 짧고 몇 개의 대기 시간만 깁니다. 왼쪽으로 치우친 데이터의 상자 그림은 수명 데이터를 보여줍니다. 몇 개의 품목이 즉시 고장나고 더 많은 품목이 나중에 고장납니다.
- 특이치
-
다른 데이터 값에서 멀리 떨어져 있는 데이터 값인 특이치는 분석 결과에 크게 영향을 미칠 수 있습니다. 일반적으로 상자 그림에서 특이치를 식별하기가 가장 쉽습니다.
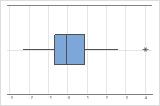
상자 그림에서는 별표(*)가 특이치를 나타냅니다.
특이치의 원인을 식별합니다. 모든 데이터 입력 오류 또는 측정 오류를 수정합니다. 비정상적인 일회성 사건에 대한 데이터 값을 삭제합니다(특수 원인이라고도 함). 그런 다음 분석을 반복합니다. 자세한 내용은 특이치 식별에서 확인하십시오.
히스토그램
히스토그램은 표본 값을 여러 구간으로 나누고 각 구간 내 데이터 값의 빈도를 막대로 나타냅니다.
해석
데이터의 모양과 산포를 평가하려면 히스토그램을 사용합니다. 히스토그램은 표본 크기가 20보다 클 때 가장 적합합니다.
- 치우친 데이터
-
정규 곡선과 겹쳐진 데이터 히스토그램을 사용하여 데이터의 정규성을 조사할 수 있습니다. 곡선으로 알 수 있듯이 정규 분포는 대칭이고 종 모양입니다. 일반적으로 표본 수가 적으면 정규성을 평가하기 어렵습니다. 확률도가 분포 적합도를 결정하기에 가장 좋습니다.
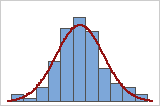
좋은 적합치
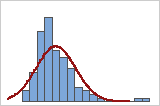
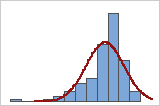
좋지 않은 적합치
- 특이치
-
다른 데이터 값에서 멀리 떨어져 있는 데이터 값인 특이치는 분석 결과에 크게 영향을 미칠 수 있습니다. 일반적으로 상자 그림에서 특이치를 식별하기가 가장 쉽습니다.
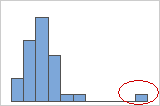
히스토그램에서는 그래프 양쪽 끝의 고립된 막대가 가능한 특이치를 나타냅니다.
특이치의 원인을 식별합니다. 모든 데이터 입력 오류 또는 측정 오류를 수정합니다. 비정상적인 일회성 사건에 대한 데이터 값을 삭제합니다(특수 원인이라고도 함). 그런 다음 분석을 반복합니다. 자세한 내용은 특이치 식별에서 확인하십시오.
- 다봉 데이터
-
다봉 데이터에는 봉우리(최빈값이라고도 함)가 여러 개 있습니다. 다봉 데이터는 보통 중요한 변수가 아직 확인되지 않았다는 것을 의미합니다.
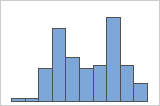
단순
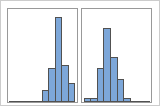
그룹 표시
예를 들어, 한 은행의 관리자가 대기 시간 데이터를 수집하여 단순 히스토그램을 생성합니다. 히스토그램에는 두 개의 봉우리가 있는 것으로 보입니다. 추가 조사 후, 관리자는 수표를 현금으로 바꾸려는 고객의 대기 시간이 부동산 융자를 신청하는 고객의 대기 시간보다 짧은 것을 확인합니다. 관리자는 고객 작업에 대한 그룹 변수를 추가한 후 그룹을 사용하여 히스토그램을 생성합니다.
관측치를 그룹으로 분류할 수 있는 추가 정보가 있는 경우 이 정보를 사용하여 그룹 변수를 만들 수 있습니다. 그런 다음, 그룹으로 그래프를 생성하여 그룹 변수가 데이터의 봉우리를 설명하는지 여부를 확인할 수 있습니다.
개별 값 그림
개별 값 그림은 표본 내 개별 값을 표시합니다. 각 원은 관측치 하나를 나타냅니다. 개별 값 그림은 관측치 수가 비교적 적고 각 관측치의 영향도 평가해야 하는 경우 특히 유용합니다.
해석
데이터의 산포를 평가하고 잠재적 특이치를 식별하려면 개별 값 그림을 사용합니다. 개별 값 그림은 표본 크기가 50보다 작을 때 가장 적합합니다.
- 치우친 데이터
-
데이터가 치우쳐 있는 것으로 보이는지 여부를 확인하려면 데이터의 산포를 조사합니다. 데이터가 치우쳐 있으면 대부분의 데이터가 그래프의 높은 쪽이나 낮은 쪽에 위치합니다. 일반적으로 히스토그램이나 상자 그림에서 왜도를 탐지하기가 가장 쉽습니다.
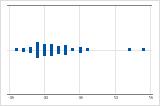
오른쪽으로 치우침
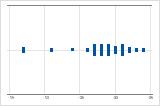
왼쪽으로 치우침
오른쪽으로 치우친 데이터의 개별 값 그림은 대기 시간을 보여줍니다. 대부분의 대기 시간이 비교적 짧고 몇 개의 대기 시간만 깁니다. 왼쪽으로 치우친 데이터의 개별 값 그림은 수명 데이터를 보여줍니다. 몇 개의 품목이 즉시 고장나고 더 많은 품목이 나중에 고장납니다.
- 특이치
-
다른 데이터 값에서 멀리 떨어져 있는 데이터 값인 특이치는 분석 결과에 크게 영향을 미칠 수 있습니다. 일반적으로 상자 그림에서 특이치를 식별하기가 가장 쉽습니다.
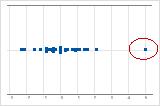
개별 값 그림에서는 비정상적으로 낮거나 높은 데이터 값이 가능한 특이치를 나타냅니다.
특이치의 원인을 식별합니다. 모든 데이터 입력 오류 또는 측정 오류를 수정합니다. 비정상적인 일회성 사건에 대한 데이터 값을 삭제합니다(특수 원인이라고도 함). 그런 다음 분석을 반복합니다. 자세한 내용은 특이치 식별에서 확인하십시오.
Q1
사분위수는 순서가 있는 데이터의 표본을 네 개의 동일한 부분으로 나누는 세 개의 값, 25%의 제1 사분위수(Q1), 50%의 제2 사분위수(Q2 또는 중위수), 75%의 제3 사분위수(Q3)입니다.
제1 사분위수는 25번째 백분위수이며 데이터의 25%가 이 값보다 작거나 같다는 것을 나타냅니다.
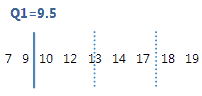
이 순서가 있는 데이터의 경우 제1 사분위수(Q1)는 9.5입니다. 즉, 데이터의 25%가 9.5보다 작거나 같습니다.
IQR
사분위간 범위(IQR)는 제1 사분위수(Q1)와 제3 사분위수(Q3) 사이의 거리입니다. 데이터의 50%는 이 범위에 포함됩니다.
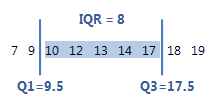
이 순서가 있는 데이터의 경우 사분위간 범위는 8(17.5–9.5 = 8)입니다. 즉, 데이터의 중간 50%는 9.5와 17.5 사이에 포함됩니다.
해석
데이터의 산포를 설명하려면 사분위간 범위를 사용합니다. 데이터의 산포가 증가하면 IQR이 더 커집니다.
최대값
최대값은 가장 큰 데이터 값입니다.
이 데이터에서 최대값은 19입니다.
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
해석
가능한 특이치 또는 데이터 입력 오류를 식별하려면 최대값을 사용합니다. 데이터의 산포를 평가하는 가장 간단한 방법은 최소값과 최대값을 비교하는 것입니다. 최대값이 아주 큰 경우에는 데이터의 중심, 산포, 모양 외에 극단값의 원인도 조사하십시오.
중위수
중위수는 데이터 집합의 중간점입니다. 중간점 값은 관측치의 반이 이 값보다 크고 관측치의 반이 이 값보다 작은 점입니다. 중위수는 관측치에 순위를 매기고 순위가 [N + 1] / 2인 관측치를 찾는 방법으로 결정됩니다. 관측치의 수가 짝수이면 순위가 N / 2인 관측치와 순위가 [N / 2] + 1인 관측치의 평균 값이 중위수입니다.
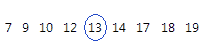
이 순서 데이터의 경우 중위수는 13입니다. 즉, 값의 반은 13보다 작거나 같고, 값의 반은 13보다 크거나 같습니다. 값이 20인 다른 관측치를 추가하는 경우 중위수는 13.5로, 5번째 관측치(13)와 6번째 관측치(14)의 평균입니다.
해석
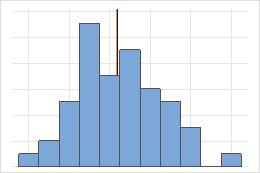
대칭
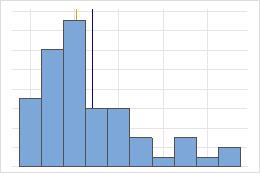
비대칭
대칭 분포의 경우 평균(파란색 선)과 중위수(주황색 선)가 너무 비슷하여 두 선을 모두 쉽게 볼 수 없습니다. 그러나 비대칭 분포는 오른쪽으로 치우칩니다.
최소값
최소값은 가장 작은 데이터 값입니다.
이 데이터에서 최소값은 7입니다.
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
해석
가능한 특이치 또는 데이터 입력 오류를 식별하려면 최소값을 사용합니다. 데이터의 산포를 평가하는 가장 간단한 방법은 최소값과 최대값을 비교하는 것입니다. 최소값이 아주 작은 경우에는 데이터의 중심, 산포, 모양 외에 극단값의 원인도 조사하십시오.
범위
범위는 표본의 최대 데이터 값과 최소 데이터 값의 차이입니다. 범위는 모든 데이터 값이 포함된 간격을 나타냅니다.
해석
데이터의 산포 정도를 확인하려면 범위를 사용합니다. 범위 값이 클수록 데이터의 산포가 크다는 것을 나타냅니다. 범위 값이 작으면 데이터의 산포가 작다는 것을 나타냅니다. 범위는 두 데이터 값만을 사용하여 계산되기 때문에 데이터 집합이 작은 경우 더 유용합니다.
Q3
사분위수는 순서가 있는 데이터의 표본을 네 개의 동일한 부분으로 나누는 세 개의 값, 25%의 제1 사분위수(Q1), 50%의 제2 사분위수(Q2 또는 중위수), 75%의 제3 사분위수(Q3)입니다.
제3 사분위수는 75번째 백분위수이며 데이터의 75%가 이 값보다 작거나 같다는 것을 나타냅니다.
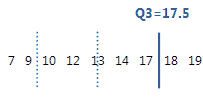
이 순서가 있는 데이터의 경우 제3 사분위수(Q3)는 17.5입니다. 즉, 데이터의 75%가 17.5보다 작거나 같습니다.
평균
평균은 모든 관측치의 합을 관측치 수로 나눈 데이터의 평균입니다.
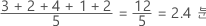
해석
데이터 중심을 나타내는 하나의 값으로 표본을 설명하려면 평균을 사용하십시오. 많은 통계 분석에서 평균을 데이터의 분포 중심에 대한 표준 측도로 사용합니다.

대칭

비대칭
대칭 분포의 경우 평균(파란색 선)과 중위수(주황색 선)가 너무 비슷하여 두 선을 모두 쉽게 볼 수 없습니다. 그러나 비대칭 분포는 오른쪽으로 치우칩니다.
SE 평균
평균의 표준 오차(SE 평균)는 같은 모집단에서 반복 표본을 추출하는 경우 얻게 될 표본 평균 간의 변동성을 추정합니다. 평균의 표준 오차는 표본 간의 변동성을 추정하는 반면, 표준 편차는 단일 표본 내의 변동성을 측정합니다.
예를 들어, 312개의 배송 시간 랜덤 표본에서 평균 배송 시간이 3.80일이고 표준 편차가 1.43일입니다. 이 숫자로 0.08일의 평균에 대한 표준 오차가 산출됩니다(1.43을 312 제곱근으로 나눈 값). 동일한 크기의 여러 랜덤 표본을 동일한 모집단에서 추출한 경우 서로 다른 표본 평균의 표준 편차는 약 0.08일이 됩니다.
해석
평균의 표준 오차를 사용하여 표본 평균이 모평균을 얼마나 정확하게 추정하는지 확인할 수 있습니다. .
평균의 표준 오차 값이 작을수록 모집단 평균의 더 정확한 추정치를 나타냅니다. 일반적으로 표준 편차가 클수록 평균의 표준 오차가 더 크고 추정치가 덜 정확합니다. 표본 크기가 클수록 평균의 표준 오차가 더 작고 모집단 평균의 추정치가 더 정확하게 됩니다.
Minitab에서는 평균의 표준 오차를 사용하여 신뢰 구간을 계산합니다.
TrMean
가장 큰 값 5%와 가장 작은 값 5%를 제외한 데이터의 평균입니다.
절사 평균을 사용하면 너무 크거나 너무 작은 값들이 평균에 영향을 미치지 않도록 할 수 있습니다. 데이터에 특이치가 있는 경우 절사 평균이 평균보다 더 나은 중심 위치의 측도일 수 있습니다.
CumN
| 학년 | 카운트 | 누적 개수 | 계산 |
|---|---|---|---|
| 1 | 49 | 49 | 49 |
| 2 | 58 | 107 | 49 + 58 |
| 3 | 52 | 159 | 49 + 58 + 52 |
| 4 | 60 | 219 | 49 + 58 + 52 + 60 |
| 5 | 48 | 267 | 49 + 58 + 52 + 60 + 48 |
| 6 | 55 | 322 | 49 + 58 + 52 + 60 + 48 + 55 |
N*
표본에 있는 결측값의 개수입니다. 결측값 개수는 결측값 기호 *가 있는 셀을 가리킵니다.
| 전체 카운트 | N | N* |
|---|---|---|
| 149 | 141 | 8 |
N
표본에 있는 비결측값의 개수입니다.
| 전체 카운트 | N | N* |
|---|---|---|
| 149 | 141 | 8 |
전체 카운트
열에 있는 관측치의 총 개수입니다. 결측값 개수와 비결측값 개수를 나타내는 데 사용합니다
| 전체 카운트 | N | N* |
|---|---|---|
| 149 | 141 | 8 |
CumPct
누적 백분율(CumPct)은 기준 변수의 각 그룹에 대한 백분율의 누적합입니다. 다음 예에서 기준 변수에는 라인 1, 라인 2, 라인 3, 라인 4 등 4개의 그룹이 있습니다.
| 그룹(기준 변수) | 백분율 | CumPct |
|---|---|---|
| 라인 1 | 16 | 16 |
| 라인 2 | 20 | 36 |
| 라인 3 | 36 | 72 |
| 라인 4 | 28 | 100 |
백분율
기준 변수의 각 그룹 내 관측치의 백분율입니다. 다음 예에는 라인 1, 라인 2, 라인 3, 라인 4 등 4개의 그룹이 있습니다.
| 그룹(기준 변수) | 백분율 |
|---|---|
| 라인 1 | 16 |
| 라인 2 | 20 |
| 라인 3 | 36 |
| 라인 4 | 28 |
첨도
첨도는 분포의 꼬리가 정규 분포와 어떻게 다른지 나타냅니다.
해석
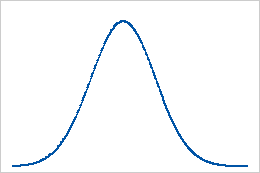
기준선: 0의 첨도 값
정규 분포를 따르는 데이터가 첨도의 기준선을 설정합니다. 첨도 값이 0이면 데이터가 완전히 정규 분포를 따른다는 것을 나타냅니다. 첨도 값이 0으로부터 유의하게 벗어나면 데이터가 정규 분포를 따르지 않는다는 것을 나타냅니다.
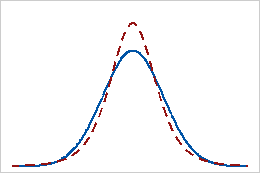
양의 첨도
분포의 첨도 값이 양수이면 분포의 꼬리가 정규 분포보다 두껍다는 것을 나타냅니다. 예를 들어, t-분포를 따르는 데이터의 첨도 값은 양수입니다. 실선은 정규 분포, 점선은 첨도 값이 양수인 분포를 보여줍니다.
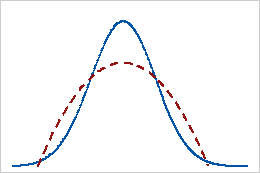
음의 첨도
분포의 첨도 값이 음수이면 분포의 꼬리가 정규 분포보다 얇다는 것을 나타냅니다. 예를 들어, 첫 번째와 두 번째 형상 모수가 2인 베타 분포를 따르는 데이터의 첨도 값은 음수입니다. 실선은 정규 분포, 점선은 첨도 값이 음수인 분포를 보여줍니다.
왜도
왜도는 데이터가 대칭이 아닌 정도입니다.
해석
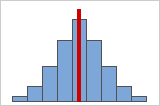
그림 A
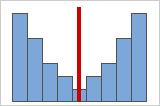
그림 B
대칭 분포 또는 치우치지 않은 분포
데이터가 대칭에 가까울수록 왜도 값이 0에 근접합니다. 그림 A는 정의에 따르면 비교적 왜도를 거의 나타내지 않는 정규 분포 데이터를 보여줍니다. 정규 데이터의 이 히스토그램 가운데에서 아래로 선을 그리면 양면이 서로 거울에 비친 이미지임을 쉽게 알 수 있습니다. 그러나 왜도 부족만으로 정규성을 의미하지는 않습니다. 그림 B는 분포의 양면이 여전히 서로 거울에 비추는 이미지이지만 데이터는 정규 분포에서 멀리 떨어져 있는 분포를 보여줍니다.
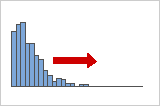
양수 또는 왼쪽으로 치우친 분포
분포의 "꼬리"가 오른쪽을 가리키고 해당 왜도 값이 0보다 크거나 양수이기 때문에 양수로 기울거나 왼쪽으로 치우친 데이터의 이름이 지정됩니다. 월급 데이터의 경우 회사의 많은 사원이 비교적 적은 월급을 받지만 점점 더 적은 사람만 매우 많은 월급을 받는 식으로 자주 치우칩니다.
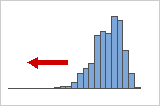
음수 또는 오른쪽으로 치우친 분포
분포의 "꼬리"가 왼쪽을 가리키고 왜도 값이 음수이기 때문에 왼쪽으로 치우치거나 음수로 기운 데이터로 지정됩니다. 고장율 데이터는 대부분 오른쪽으로 치우칩니다. 너무 적은 수의 전구만 바로 꺼지고 대다수는 오랫동안 켜져 있습니다.
CoefVar
변동 계수(CoefVar)는 평균에 상대적인 데이터의 변동을 설명하는 산포의 측도입니다. 변동 계수는 값이 단위가 없는 척도로 표시되도록 조정됩니다. 변동 계수는 이렇게 조정되기 때문에 표준 편차 대신 단위가 다르거나 평균이 매우 다른 데이터의 변동성을 비교하는 데 사용할 수 있습니다.
해석
변동 계수가 클수록 데이터의 산포가 더 큽니다.
| 큰 용기 | 작은 용기 |
|---|---|
| CoefVar = 100 * 0.4컵 / 16컵 = 2.5 | CoefVar = 100 * 0.08컵 / 1컵 = 8 |
표준 편차
표준 편차는 산포, 즉 데이터가 평균을 중심으로 퍼져 있는 정도를 나타내는 가장 일반적인 측도입니다. 모집단의 표준 편차를 나타내는 데는 σ(시그마) 기호를 자주 사용하는 반면, 표본의 표준 편차를 사용하는 데는 s를 사용합니다. 랜덤이 아니거나 공정에 자연스럽지 못한 변동은 종종 잡음이라고 합니다.
표준 편차는 데이터와 단위가 같기 때문에 일반적으로 분산보다 더 쉽게 해석할 수 있습니다.
해석
데이터가 평균을 중심으로 퍼져 있는 정도를 확인하려면 표준 편차를 사용합니다. 표준 편차 값이 클수록 데이터가 더 퍼져 있다는 것을 나타냅니다. 정규 분포에 대한 일반 규칙은 대략 68%의 값이 평균으로부터 1 표준 편차 거리 내에 있고, 95%의 값이 2 표준 편차 거리 내에 있고, 99.7%의 값이 3 표준 편차 거리 내에 있다는 것입니다.
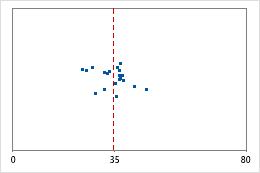
병원 1
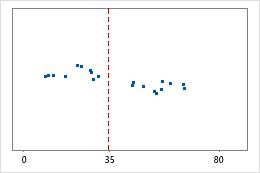
병원 2
병원 퇴원 시간
관리자들이 두 개 병원의 응급실 부서에서 치료한 환자의 퇴원 시간을 추적하고자 합니다. 평균 퇴원 시간은 동일하지만(35분) 표준 편차는 유의하게 다릅니다. 병원 1의 표준 편차가 약 6이며, 평균적으로 환자의 퇴원 시간은 평균(대시선)에서 약 6분 정도 멀어집니다. 병원 2의 표준 편차는 약 20입니다. 평균적으로 환자의 퇴원 시간은 평균(대시선)에서 약 20분 정도 멀어집니다.
분산
분산은 데이터가 평균 주위에 분산된 정도를 측정합니다. 분산은 표준 편차의 제곱과 같습니다.
해석
분산이 클수록 데이터의 범위가 더 커집니다.
분산(σ2)은 제곱된 양으로, 단위도 제곱되기 때문에 실제로 사용하기 어려울 수도 있습니다. 표준 편차는 데이터와 단위가 같기 때문에 일반적으로 더 쉽게 해석할 수 있습니다. 예를 들어, 버스 정류장에서 대기 시간의 표본을 추출한 결과 평균이 15분이고 분산은 9분2입니다. 분산은 데이터와 단위가 같지 않기 때문에 보통 제곱근(표준 편차)으로 표시됩니다. 9분2의 분산은 3분의 표준 편차와 동일합니다.
최빈값
최빈값은 관측치 집합에서 가장 자주 발생하는 값입니다. Minitab에서는 최빈값과 같은 데이터 점의 수도 표시합니다.
평균과 중위수를 구하려면 계산이 필요하지만 최빈값은 데이터 집합에서 각 값이 발생하는 횟수를 세면 됩니다.
해석
최빈값은 평균 및 중위수와 함께 사용하여 데이터 분포의 전체적인 특성을 나타낼 수 있습니다. 최빈값은 또한 데이터의 문제를 식별하기 위해 사용할 수 있습니다.
예를 들어, 최빈값이 두 개 이상인 분포는 표본에 두 모집단의 데이터가 포함되어 있다는 것을 나타낼 수도 있습니다. 데이터에 두 개의 최빈값이 포함되어 있는 경우 분포가 이봉입니다. 데이터에 세 개 이상의 최빈값이 포함되어 있는 경우에는 분포가 다봉입니다.
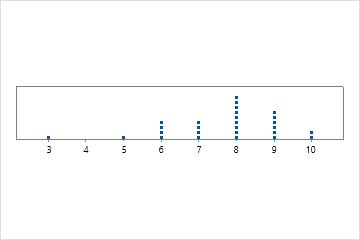
단봉
최빈값이 8 하나뿐이며 가장 자주 발생합니다.
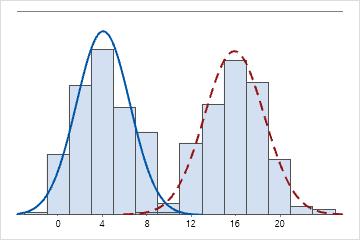
이봉
4와 16, 두 개의 최빈값이 있습니다. 데이터가 2개의 서로 다른 분포를 나타내는 것으로 보입니다.
MSSD
MSSD는 연속 차이의 제곱 평균입니다. MSSD는 분산의 추정치입니다. MSSD의 한 가지 가능한 용도는 일련의 관측치가 랜덤인지 여부를 검정하는 것입니다. 품질 관리에서 MSSD의 한 가지 가능한 용도는 부분군 크기 = 1일 때 분산을 추정하는 것입니다.
합
합은 모든 데이터 값의 합입니다. 합은 또한 평균, 표준 편차 등 통계 계산에도 사용됩니다.
제곱합
수정되지 않은 제곱합은 각 열의 값을 제곱한 다음 제곱 값의 합을 구하여 계산됩니다. 예를 들어, 열에 x1, x2, ... , , xn이 포함되어 있는 경우 제곱합은 (x12 + x22 + ... + xn2)입니다. 수정 제곱합과 달리 수정되지 않은 제곱합에는 오차가 포함됩니다. 데이터 값은 먼저 평균을 빼지 않은 제곱입니다.
